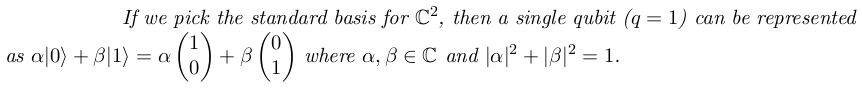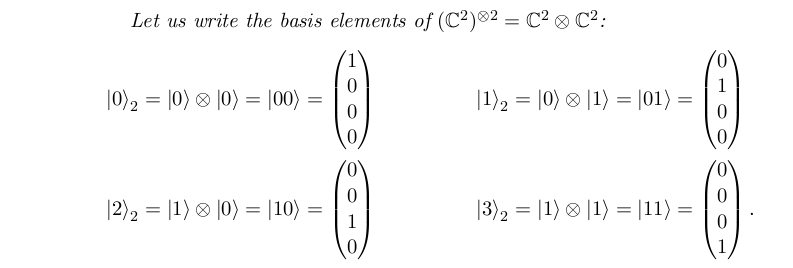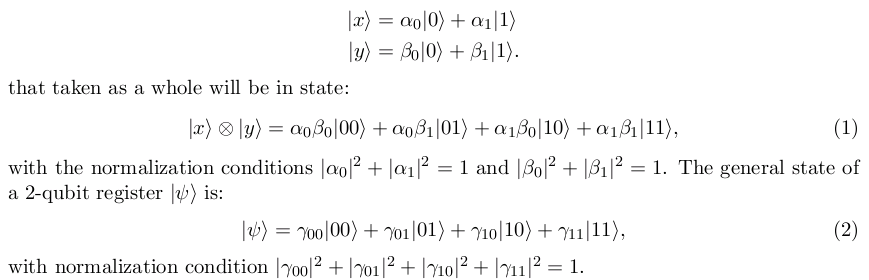Quantum Computing
-
Quantum Computing is an intriguing topic as it breaks the traditional
paradigms of 1's & 0's with qubits that can be either or both at once.
If the hyperbole in the press were to be believed, we will all soon be
walking around with supercomputers the size of a watch that can break any
existing cryptography. Of course, you need to keep your watch cooled to
a fraction of a degree above absolute zero.
-- Don Herres
010000101110011010100111101101101110100110111111000010101000100110101001101110101101100010100111100000111111010010100001101000101011111111100010101100111111100000101011011110011010101101111111
---
-
-
Goal
- Simulate quantum algorithms at a high-level,
to test correctness and evaluate performance
Outline
- History of Computing
- Quantum Physics
- Mathematical Representations
- Superdense Coding Simulation
- Addition Simulation
- Grover's Search Algorithm
- Shor Factoring Algorithm
---
Eniac 1950: 30 tons, 150 KW, 1 KB, 100 KHz

---
Phone 2018: 5 oz., 1 W, 4 GB, 2 GHz

---
QC 2018: tons, KW, 20 Qubit (220 = 1 Mb), 1 MHz

---
QC 2050: ???

---
Ion Trap Quantum Device
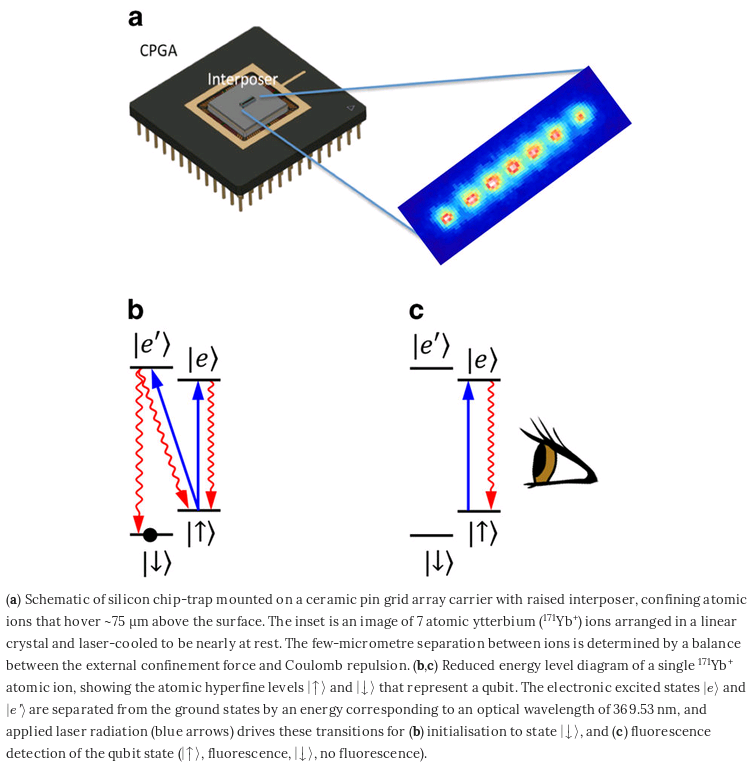
Co-designing
a scalable quantum computer with trapped atomic ions,
Kenneth R Brown, Jungsang Kim & Christopher Monroe,
Nature 2016.
---
Quantum Key Distribution
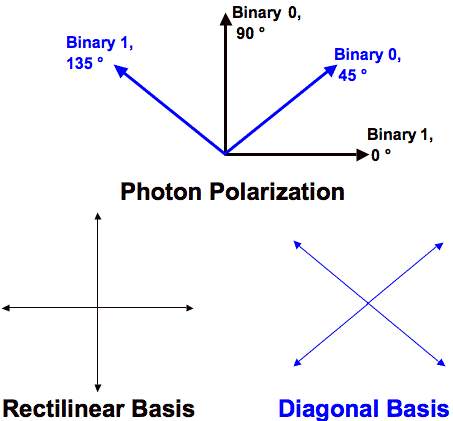
A
Survey of the Prominent Quantum Key Distribution Protocols,
Mart Haitjema. Figure 2, corrected.
---
Quantum Key Distribution
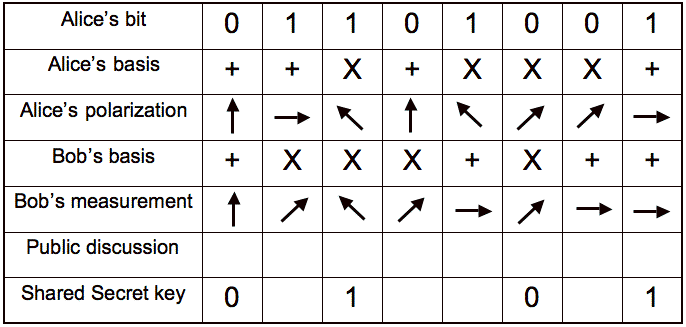
A
Survey of the Prominent Quantum Key Distribution Protocols,
Mart Haitjema. Figure 3.
---
One Qubit

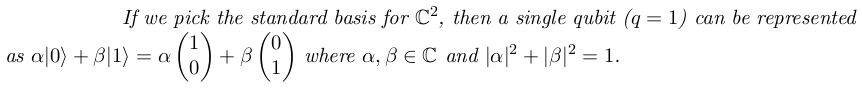
Superposition: α |0> + β |1>
Complex Amplitudes: α, β
Probabilities: |α|2, |β|2
An Introduction to Quantum Computing,
Without the Physics, Giacomo Nannicini, 2017.
---
Single Qubit Operations

Superposition
An Introduction to Quantum Computing,
Without the Physics, Giacomo Nannicini, 2017.
---
Two Qubits
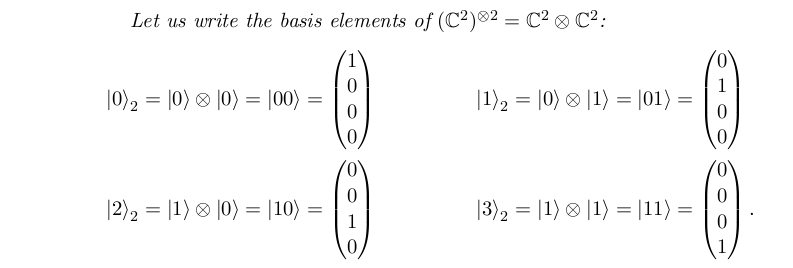
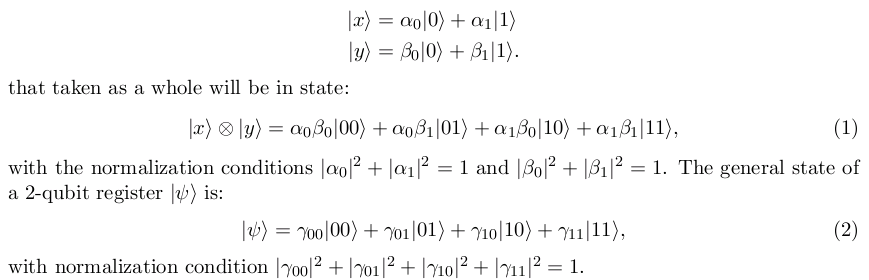
Entanglement
An Introduction to Quantum Computing,
Without the Physics, Giacomo Nannicini, 2017.
---
CNOT - entangled states
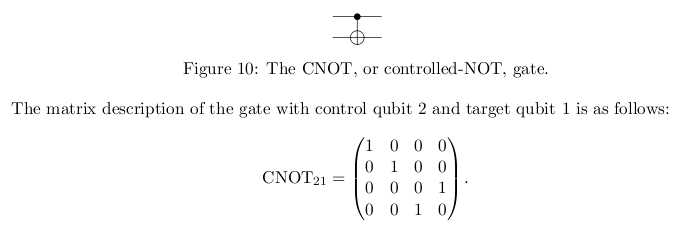
~ q a b -> a b⊕a class TwoQubit:
~ 0 0 0 0 0 def cnot(self):
~ 1 0 1 0 1 '''Controlled NOT operation'''
~ 2 1 0 1 1 self.onezero, self.oneone = self.oneone, self.onezero
~ 3 1 1 1 0 return self
~ Using an array: Using names for the complex amplitudes:
~ q[0], q[1], q[2], q[3] zerozero, zeroone, onezero, oneone
~ swap q[2] and q[3] Python Quantum Computing simulator, Juliana Peña, 2011.
---
Superdense Coding Protocol
-
Eve starts with two qubits in state |00>
Eve prepares Bell state, first with Hadamard gate on first qubit: 0.707 |00> + 0.707 |10>
and then with controlled Not gate on the two qubits: 0.707 |00> + 0.707 |11>
Eve sends one qubit to Alice and another to Bob.
Alice wants to encode two classical bits to send to Bob with only her one qubit
First bit: 1 Second bit: 0
For encoding 10, the Z gate is applied: 0.707 |00> + -0.707 |11>
Because Alice and Bob's qubits were entangled by Eve,
Alice's operations affect both, despite being far apart.
Alice sends her qubit to Bob. If someone intercepts and measures the qubit,
Now Bob has both original qubits. they measure |0> and |1> with equal probability,
Bob applies a reverse operation of regardless of the bits encoded by Alice.
Eve's original operation
First a controlled Not: 0.707 |00> + -0.707 |10>
Then a Hadamard on the first qubit: |10>
Finally, Bob measures the qubits in the computational basis.
The result of Bob's measurement is (1,0), Alice's two bits.
Python
Quantum Computing simulator, Juliana Pena, 2011.
---
-
Simulating Two Qubits - C Code
-
// CNOT, swap q[2] and q[3]
//
// Python: self.onezero, self.oneone = self.oneone, self.onezero
//
void CNOT( double complex q[4])
{
~ double complex t = q[3]; q[3] = q[2]; q[2] = t;
}
// Z gate on first qubit
//
// Python: self.onezero *= -1; self.oneone *= -1
//
void Z( double complex q[4])
{
~ q[2] = -q[2]; q[3] = -q[3];
}
Python
Quantum Computing simulator, Juliana Pena, 2011.
---
Low-level Simulation
6-bit adder
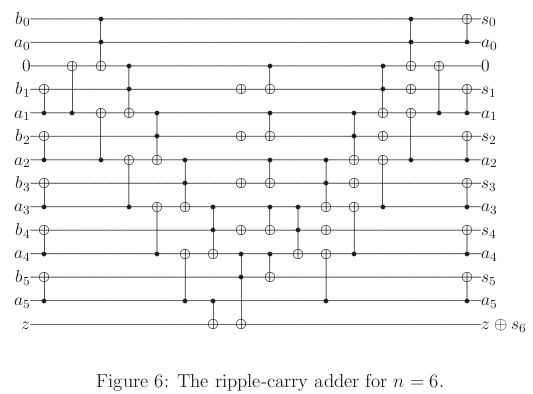
A new quantum ripple-carry addition circuit,
Steven A. Cuccaro, Thomas G. Draper, Samuel A. Kutin, David Petrie Moulton, 2004.
---
-
High-level Simulation
-
Addition mod M: (a,b) -> (a,(a+b)%M)
- a and b are m-qubit pieces of an n-qubit register q,
- with n=2m, N=2n, and M=2m
-
t = copy(q); // temporary copy of q register
for( X = 0; X < N; ++X) // for each element of the state array
{
~ a = X >> m; // top m bits
~ b = X & mask; // bottom m bits, mask = 2m-1 = 0111..1 (m 1's)
~ c = (a + b) % M; // classical addition
~ Y = (a << m) | c; // concatenate the bits
~ q[Y] = t[X]; // perform the permutation
}
Quantum Computing Emulation, R. Perry, 2018
---
-
High-level Function Implementation in a Simulator
- Modular addition implemented as a permutation
- Modular exponentiation and other periodic functions
also implemented as permutations
- Quantum Discrete Fourier Transform implemented
using classical FFT on the state amplitudes
- Other operations implemented directly on the state amplitudes
- Resulting quantum state is the same regardless of whether it is simulated
at a low-level or high-level
- Physical quantum system: measurement collapses system to one state
- Simulation: can view all of the state amplitudes directly
---
-
Grover's Search - Quadratic Speedup
- Search space of size 2n using 2n/2
function evaluations vs. classical 2n/2
- Security implications: 256-bit key for ANY algorithm will
have only 128-bit security level
-
~ for( iter = 1; iter <= k; ++iter)
~ {
~ // apply f, i.e. flip sign of state m
~ //
~ q[m] = -q[m];
~ // inversion about the average
~ //
~ avg = 0; for( i = 0; i < N; ++i) avg += q[i];
~ avg *= 2.0/N; for( i = 0; i < N; ++i) q[i] = avg - q[i];
~ }
Quantum Computing Emulation, R. Perry, 2018
---
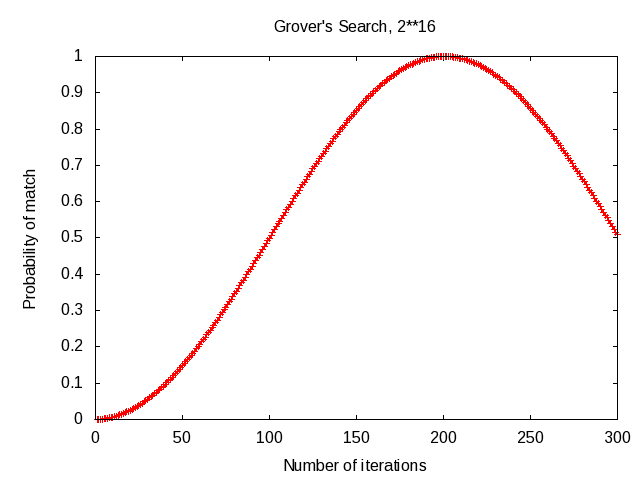
-
Grover's Search - 16-bit Example
- 216 = 65536 possibilities,
would take (216)/2 = 32768 iterations on average classically
-
Takes only (π/4)216/2 = 201 quantum iterations optimally,
success probability 0.999988
Quantum Computing Emulation, R. Perry, 2018
---
-
Shor factoring - breaks RSA
- Quantum evaluation of
ya mod N
for random y, and ALL a at once
- Determine period r, mod N:
yr = 1, so (yr/2 - 1)*(yr/2 + 1) = 0
-> will share factor with N
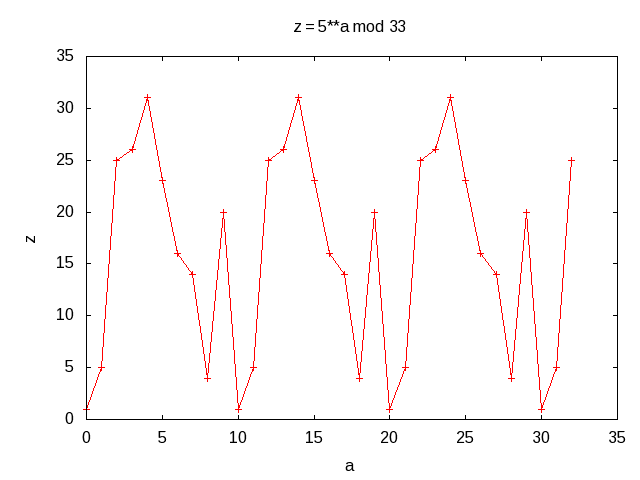
Quantum Computing Emulation, R. Perry, 2018
---
-
Shor factoring example, N = 33
- DFT probability peaks (205, 410, 614, 819, ...) produce period estimates
(9.9902, 4.9951, 3.3355, 2.5006, ...)
- Using r = 10 ≈ 9.9902: (510/2 - 1)*(510/2 + 1) = 22*24
- gcd(22,N) = 11, gcd(24,N) = 3, both factors of N
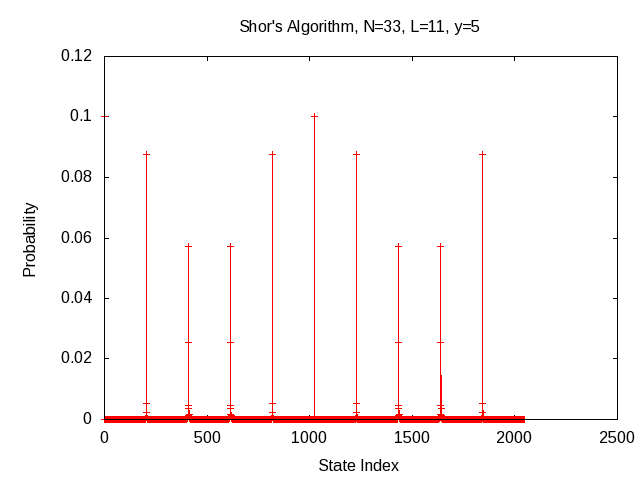
Quantum Computing Emulation, R. Perry, 2018
---
-
References
- An Introduction to Quantum Computing,
Without the Physics, Giacomo Nannicini, 2017.
arxiv.org/abs/1708.03684
- Python
Quantum Computing simulator, Juliana Pena, 2011.
Two qubits and superdense coding protocol example.
gist.github.com/limitedmage/945473
- Quantum Computing Emulation, R. Perry, 2018.
fog.misty.com/perry/qce/notes.html
Hackers of the Future
Already planning attacks on quantum computers which do not yet exist:
- An entangling-probe attack on Shor's algorithm for factorization, Hiroo Azuma, 2017.
arxiv.org/abs/1705.00271 :
an attacker can steal an exact solution of Shor's algorithm outside
an institute where the quantum computer is installed if he replaces its
initialized quantum register with entangled qubits.
---

https://www.ias.edu/ideas/2014/ambainis-quantum-computing
https://atelier.bnpparibas/en/health/article/quantum-computing-set-revolutionise-health-sector