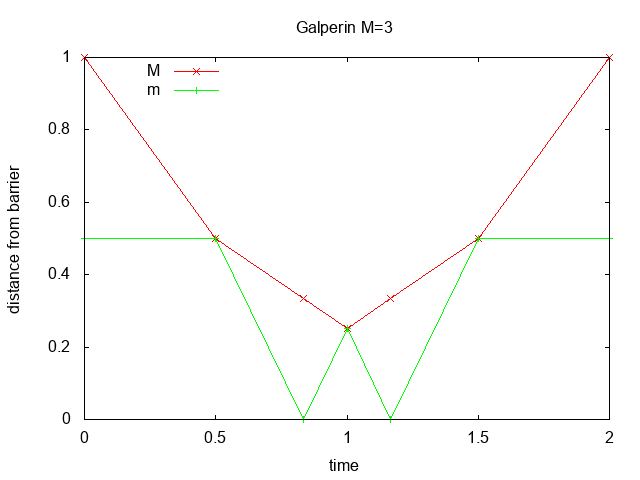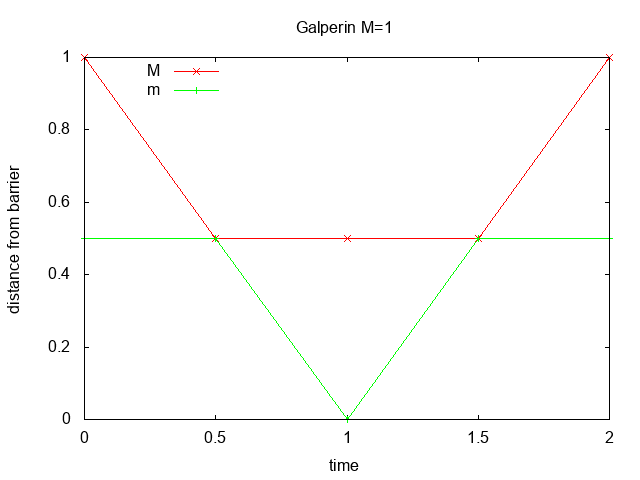
In 2003 Galperin discovered a relationship between bouncing blocks and the digits of π [1]. Recently Brown demonstrated an exact isomorphism between Galperin's bouncing blocks and Grover's algorithm for quantum search [2,3]. Here we show some analysis and simulation results for Galperin bouncing blocks and the Grover search analogy.

Consider two blocks of mass M and m, with normalization m=1 so M represents the mass ratio. Initially block m is stationary and block M is moving with constant velocity down (in zero gravity) towards block m above a barrier. There is no friction and collisions are elastic so momentum and kinetic energy are conserved.

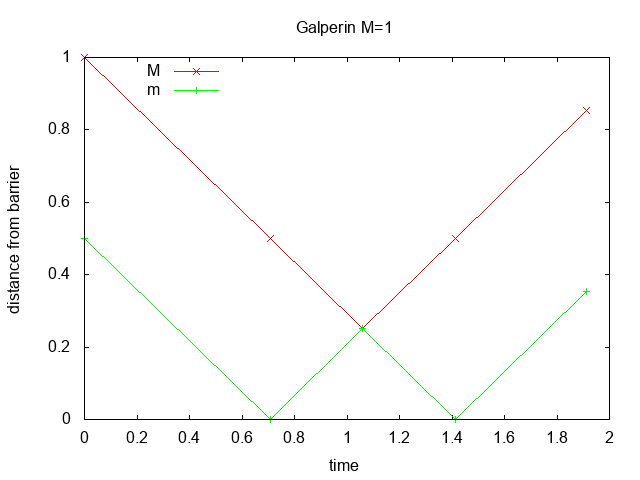
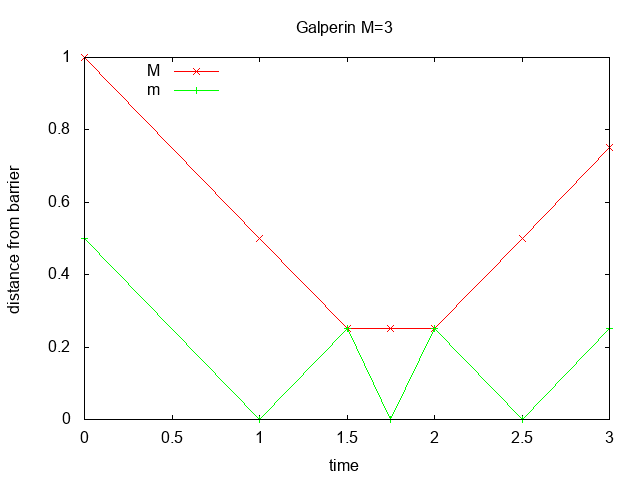
Figure 1 shows the distance from the barrier vs. time for M=1 and M=3. If the masses are equal (M=1) there are 3 collisions: first between M and m, leaving M stationary while m continues towards the barrier; second when m bounces off of the barrier; and third when the blocks collide again leaving m stationary and M moving upwards. If M=3 there are 5 collisions.

Figure 1: distance vs. time for M=1 and M=3

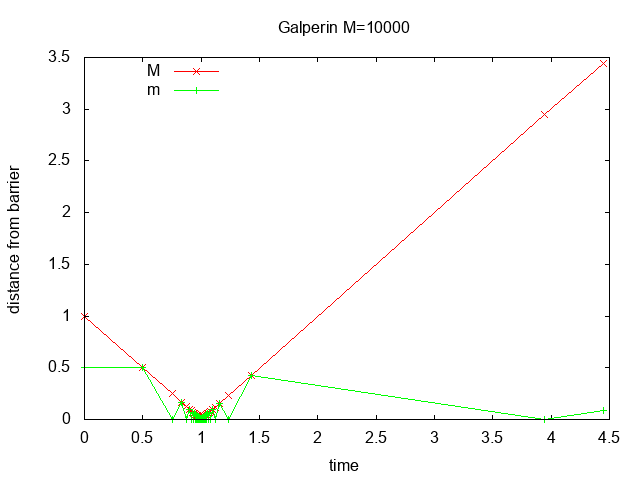
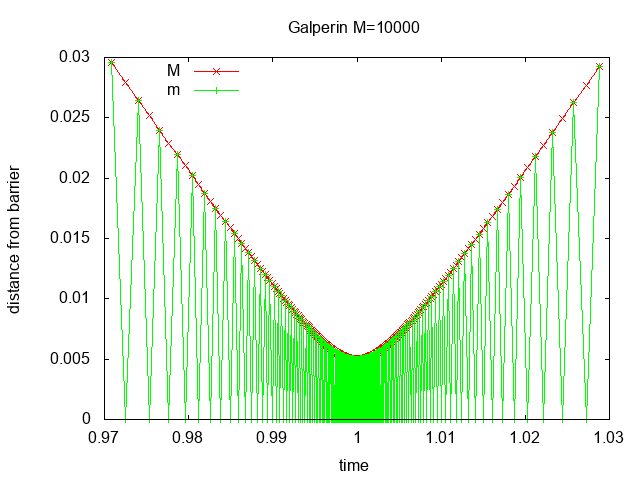
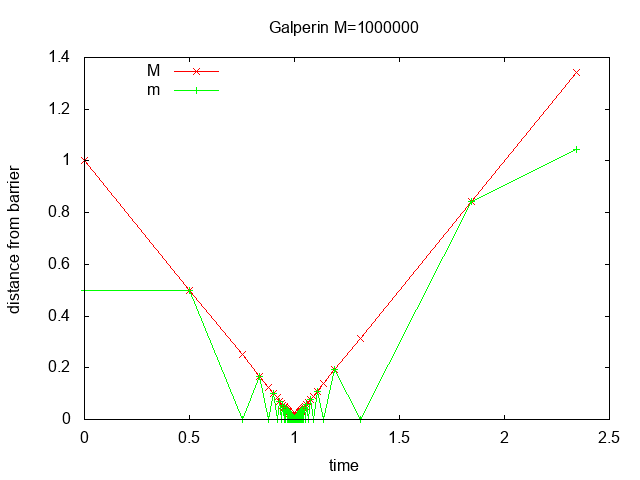
Galperin proved that if M=100N then the number of collisions is the first N+1 digits of π [1]. With M=1 (N=0) there are 3 collisions, with M=100 (N=1) there are 31 collisions, with M=10000 there are 314 collisions, with M=1000000 there are 3141 collisions, etc.

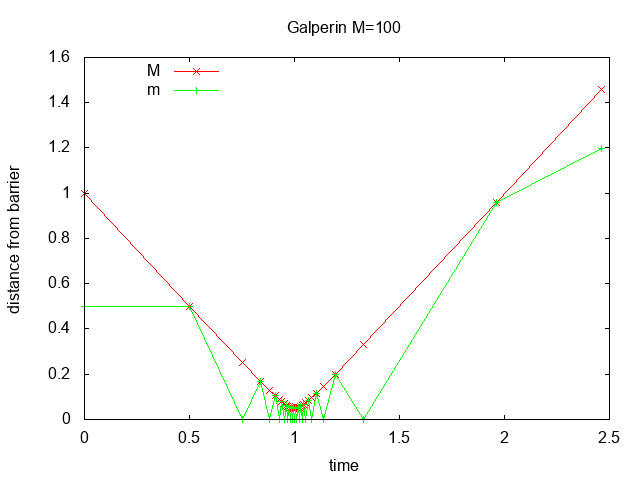
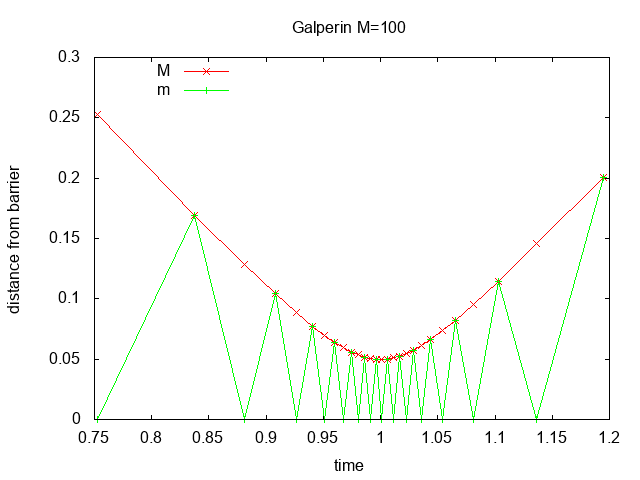
Figure 2 shows the distance from the barrier vs. time for M=100, 10000, 1000000 with zoom in at time=1. Most of the collisions occur when block M is close to the barrier and block m bounces quickly back and forth transferring momentum until block M reverses direction.

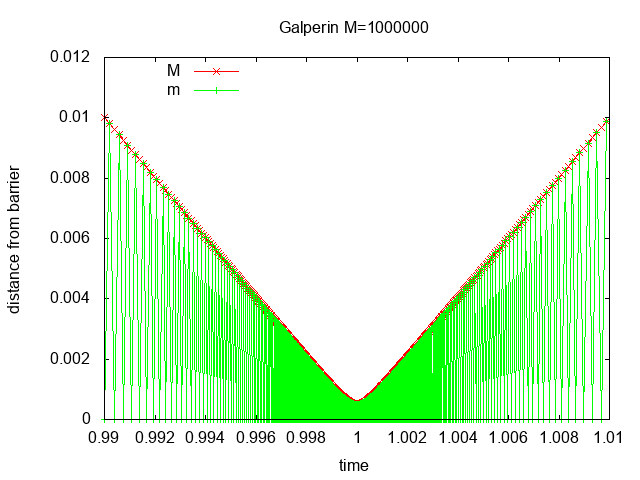Figure 2: distance vs. time for M=100, 10000, 1000000 with zoom in at time=1

A derivation of the formulas used to produce Figures 1 and 2 is in the Appendix, and the source code is pi.c.

Brown demonstrated an exact isomorphism between Galperin's bouncing blocks and Grover's algorithm for quantum search [2]. The analogy uses a d-state quantum system with d=M+1 such that one state represents mass m and the remaining d-1 states represent mass M. Rather than block m starting stationary, the blocks begin with equal velocities -1/sqrt(d) corresponding to an initial equal superposition of the quantum states. The number of collisions is still equal to the digits of π.

The quantum state amplitudes correspond to the velocities of the blocks, and based on the velocities a pseudo "distance from the barrier" can be computed for comparison with the Galperin scenario. The magnitude-squared of the amplitude of state m represents the probability of a measurement yielding the desired state.

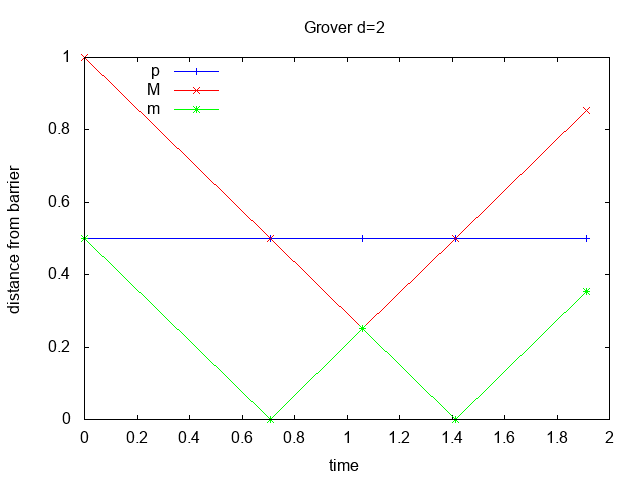
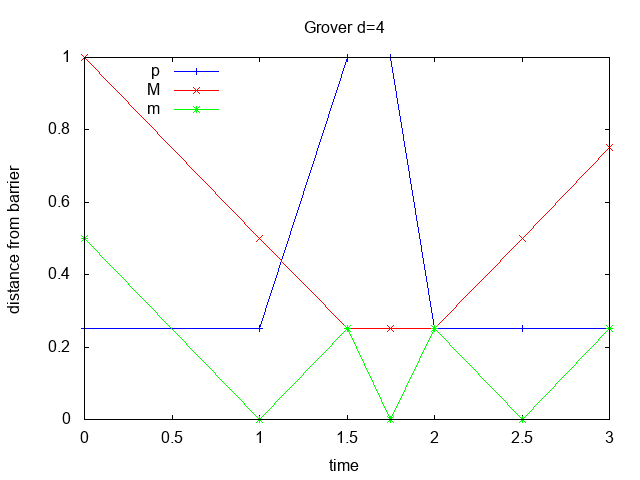
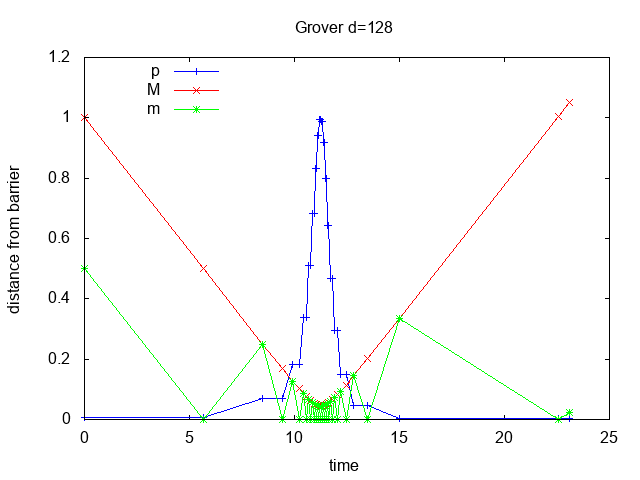
Figure 3 shows the distance from the barrier and Grover probability vs. time for d=2, 4, 128 corresponding to Galperin M=1, 3, 127. In all cases the Grover and Galperin distance values are identical even though they were computed using separate programs and seemingly different algorithms.

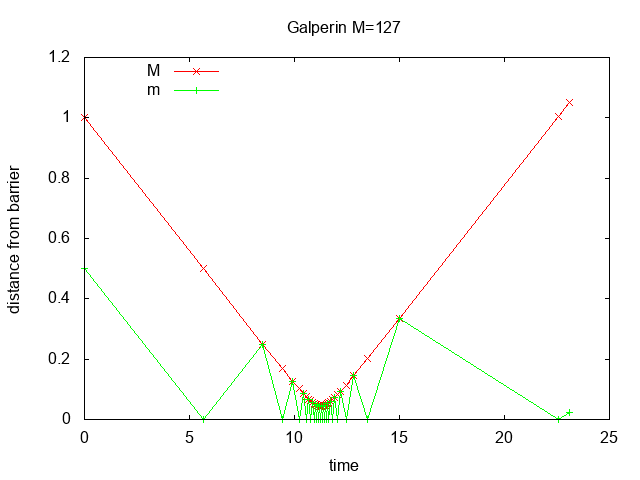Figure 3: distance and Grover probability p vs. time for Grover and Galperin scenarios

The Grover algorithm step which flips the sign of state m is exactly the same as the Galperin block m bouncing off of the barrier, i.e. u'=-u, where u and u' are the original and reflected velocities of block m.

And the Grover algorithm step which performs inversion about the mean is exactly the same as the Galperin blocks m and M colliding:

  a = (sum of all amplitudes)/(M+1)

    = (u+Mv)/(M+1)

 v' = 2a - v

    = 2(u+Mv)/(M+1) - v

    = (u+Mv + u-v)/(M+1)

 v' = (P + (u-v))/(M+1),  with P=u+Mv

The Grover simulation source code is Grover.cc, part of qce++.

[1] Playing pool with π, G. Galperin, Regular and Chaotic Dynamics, v.8, no.4, 2003.

[2] Playing Pool with |ψ>: from Bouncing Billiards to Quantum Search, Adam R. Brown, 30 Oct. 2020. Errata: in the section "One Hit Wonder", when M=3 the light ball is actually never stationary; rather the large ball is stationary after the second collision, and then after two more collisions both balls move with equal velocities. See Figure 3.

[3] Bouncing Balls and Quantum Computing, Don Monroe, CACM, Oct. 2020.

Additional references, added 4 July 2021:

The dynamics of digits: Calculating pi with Galperin's billiards, X. M. Aretxabaleta, M. Gonchenko, N. L. Harshman, S. G. Jackson, M. Olshanii, G. E. Astrakharchik, 4 April 2020. A comprehensive review and some new results.

A Classical π Machine and Grover's Algorithm, Jiang Liu, 29 Jan 2020. A short derivation independent from [2].

Let m=1, so M is the ratio of original masses M/m.

Block m is at position x with velocity u, block M is at position y with velocity v.

blocks m and M colliding
------------------------
u and v satisfy:

 u + Mv = P  (momentum)

  u = P - Mv

 u^2 + Mv^2 = E  (energy)

  (P-Mv)^2 + Mv^2 = E

  (M^2+M)v^2 - (2PM)v + (P^2-E) = 0

After a collision, there are two solutions for new u and v (u' and v'):

 v' = (2PM +- sqrt((2PM)^2 - 4(M^2+M)(P^2-E))) / (2(M^2+M))

 v' = (P +- D) / (M+1)

  D = sqrt( ((M+1)E-P^2)/M ) = sqrt( ((M+1)(u^2+Mv^2)-(u+Mv)^2)/M )

    = sqrt( (u-v)^2 ) = +- (u-v)

First solution: u and v unchanged, blocks pass through each other:

 v' = (P - (u-v))/(M+1) = v 

Second solution: blocks bounce off each other:

 v' = (P + (u-v))/(M+1)

 u' = P - Mv';

Time and location of collision:

 x + u*dt = y + v*dt

  dt = (y-x)/(u-v)

  x' = y' = x + u*dt

block m colliding with barrier
------------------------------
u and v satisfy:

 u + Mv = P

After collision:

 u' = -u

 P' = u' + Mv

Time and location of collision:

 0 = x + u*dt

  dt = -x/u 

  x' = 0,  y' = y + v*dt