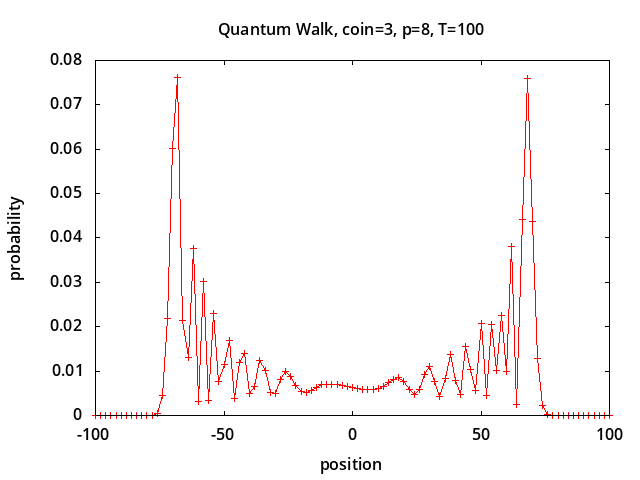Analysis and simulation results are shown for a quantum walk on a line and quantum pagerank.

A finite quantum walk in 1 dimension can be simulated using p qubits to represent a ring of P=2p positions. Starting in the middle of the ring, at position P/2, up to P/2 walk steps can be performed before wrap-around occurs.

The discrete quantum walk also uses a "coin" qubit which influences the step direction similar to a coin flip in a classical random walk. The coin qubit can be "flipped" in an balanced manner using a Hadamard transformation.

Representing the combined position/coin qubit state as |i,c>, where i ∈ {0,...,P-1} and c ∈ {0,1}, each step of the quantum walk is the operation S⋅(I⊗H)⋅|i,c> with:

  S⋅|i,0> = |i+1,0>,  move right

  S⋅|i,1> = |i-1,1>,  move left

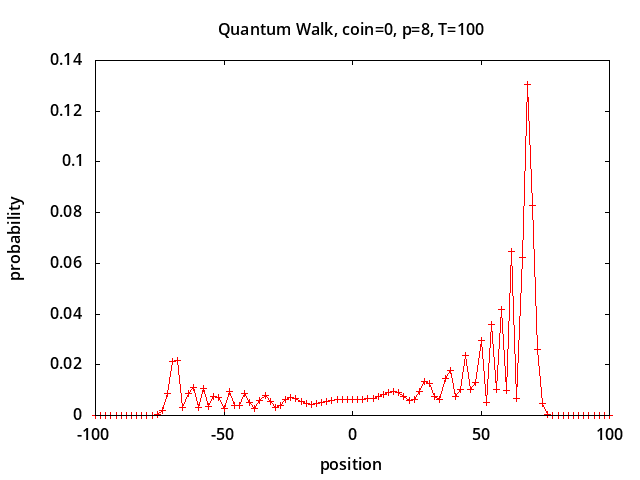
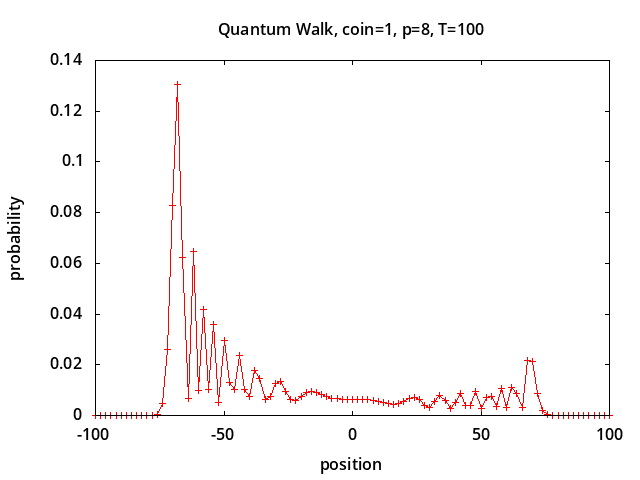
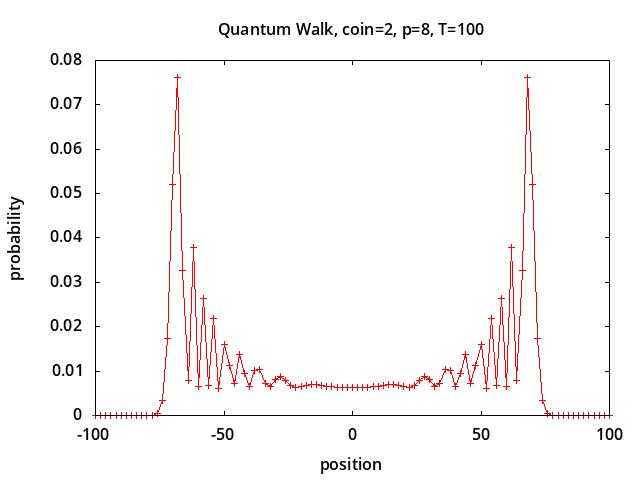
Figure 1 shows simulation results using QCE/QW1.c for quantum walks with different coin initial conditions corresponding to figures 5 and 6 from [1] and figures 4 and 5 from [2]:

Figure 1: 100-step Hadamard walks with different coin initial conditions

Position probabilities are shown after 100 steps using a Hadamard coin. A ring of size 28=256 is used, and position 0 corresponds to the center of the ring. Coin initial conditions corresponding to coin=0,1,2,3 are: |0>, |1>, (|0>+i|1>)/√2, √0.85|0>-√0.15|1>.

Depending on the coin initial conditions the walk may drift to the right or left or both, unlike a classical random walk which would have a Gaussian distribution centered around position 0.

The potential for algorithmic speedup using quantum walks has been known for some time [3]. Recently a quantum walk for ranking nodes on a network was presented by Chawla et. al. which uses only 1+⌈log2(N)⌉ qubits for N nodes, however it requires classical computation of the singular value decomposition of the N-by-N node adjacency matrix [4]. Previously a quantum pagerank algorithm was described by Paparo et. al. using 2⌈log2(N)⌉ qubits [5-7] based on Szegedy's procedure to quantize Markov chains [8]. Simulation of the Paparo algorithm uses O(N2) space for the qubit state amplitudes, but no SVD is required.

The quantum pagerank algorithms are not necessarily designed to be run on a physical quantum computer because the ranks are state probabilities which can not be directly measured. Also, the quantum walk probabilities oscillate rather than converging to fixed values, so averaging must be performed to obtain meaningful results. These algorithms are most easily implemented using simulation which allows direct access to all of the internal state amplitudes.

To calculate quantum pageranks, Paparo uses an analytical expression derived from an eigenvalue decomposition [5]. Here we will use Paparo's quantum walk operator directly in a quantum computing emulation, QCE/QW-PR.c. This is similar in form and complexity to calculation of the classical pagerank using the eigenvector power method. Quantum pagerank computation is not necessarily more efficient than classical methods, but it may be more stable with respect to parameter variations and may also have other desirable properties [6].

Each time step consists of the unitary operation:

  U2 = S⋅(2P-I)⋅S⋅(2P-I)

In a quantum simulation the swap operator can be implemented by simply swapping the from/to portions of the state amplitude indices in the projector computation, so a complete time step looks like this in C:

 // first half of time step
 //
  for( i = 0; i < N; ++i) // for each node (from)
  {
    j = i << n;  v = 0; // n is ⌈log2(N)⌉

    for( k = 0; k < N; ++k) { p = j|k; v += g[p]*q[p]; }

    for( k = 0; k < N; ++k) { p = j|k; q[p] = 2*g[p]*v-q[p]; }
  }

 // second half of time step, using reversed upper/lower state indices on q
 //
  for( i = 0; i < N; ++i) // for each node (from)
  {
    j = i << n;  v = 0;

    for( k = 0; k < N; ++k) { p = j|k; r = (k<<n)|i; v += g[p]*q[r]; }

    for( k = 0; k < N; ++k) { p = j|k; r = (k<<n)|i; q[r] = 2*g[p]*v-q[r]; }
  }

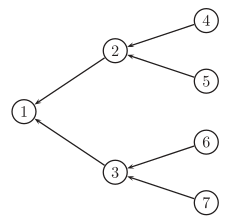Three Level Tree [5]

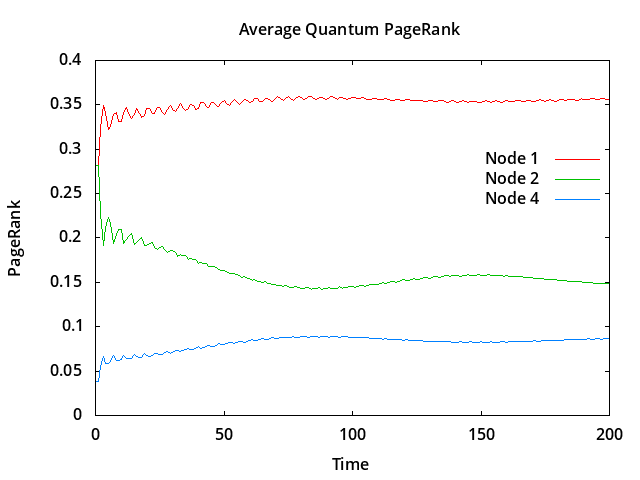Figure 2: Three Level Tree Quantum PageRank Simulation

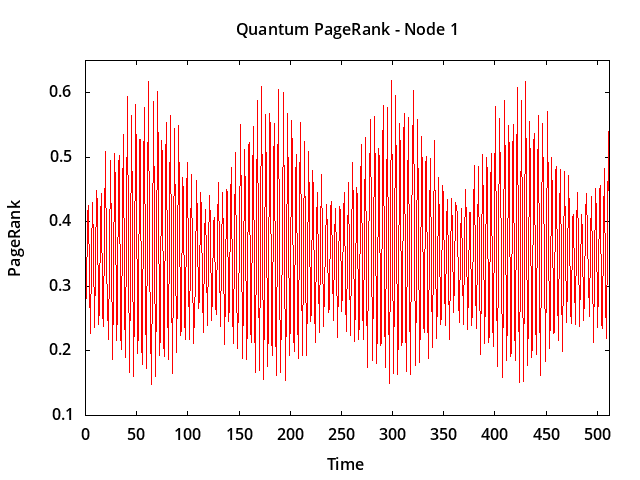
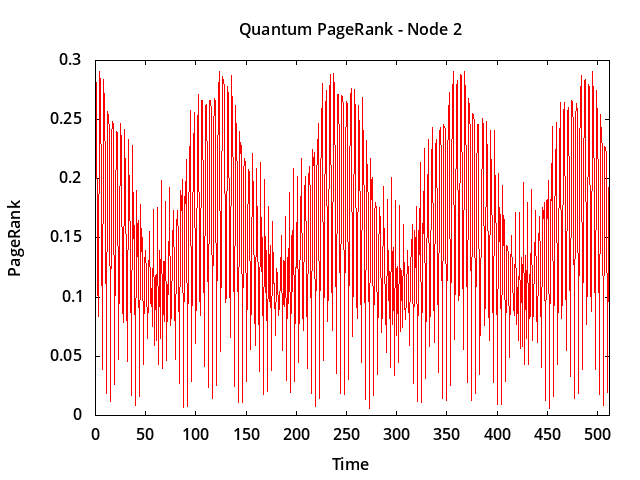
Although the quantum walk probabilities oscillate continuously over a wide range of values over time, the running average is more stable, and the node ranking order (1, 2, 4 in this example) is stable after just a few time steps.

The node ranking order in this example agrees with the classical pagerank (computed using GG.m):

  Node  Classical  Node  Quantum
     1  0.372916      1  0.355765
     2  0.180120      2  0.148449
     4  0.066711      4  0.086834

Table 1: Three Level Tree Classical and Quantum PageRank Sorted by Rank, Time=200

Figure 3 shows simulation results using QCE/QW-PR.c for the seven node network from [4] and [5]:

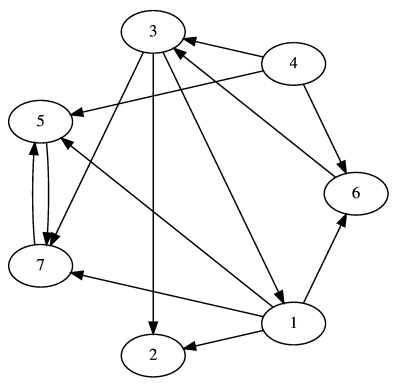Seven Node Network [4]

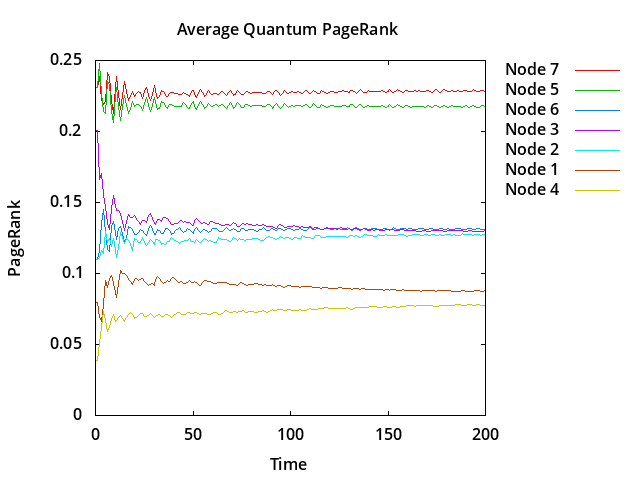Figure 3: Seven Node Network Quantum PageRank Simulation

The node ranking order in this example differs from the classical pagerank for node #6:

  Node  Classical  Node  Quantum
     7  0.369889      7  0.228401
     5  0.362387      5  0.217391
     3  0.077924      6  0.131202
     2  0.061860      3  0.130550
     1  0.051019      2  0.127290
     6  0.047981      1  0.087718
     4  0.028940      4  0.077448

Table 2: Seven Node Network Classical and Quantum PageRank Sorted by Rank, Time=200

For a larger example, a 4000 node random graph was generated using QCE/graph.c. Nodes 1, 2, and 3 act as hubs, with probabilities of connections 0.2, 0.15, and 0.1 respectively from the other nodes, and additionally all nodes have up to 40 other outgoing connections to randomly selected nodes.

Figure 4 shows that nodes 1, 2, and 3 are ranked in order starting at time 0, also that node 10 is somewhat highly ranked, considering just nodes 1 to 50:

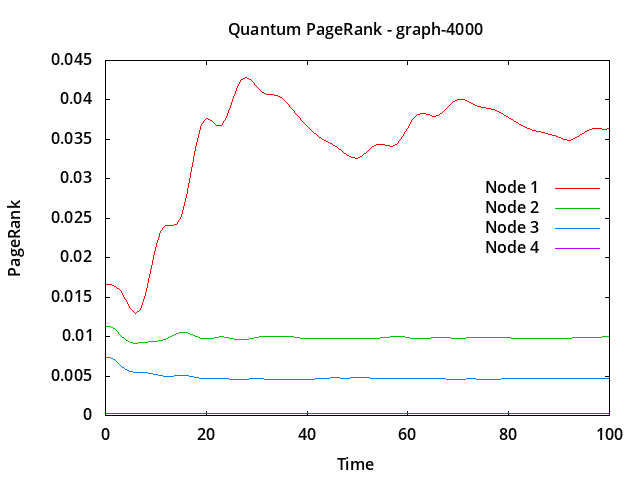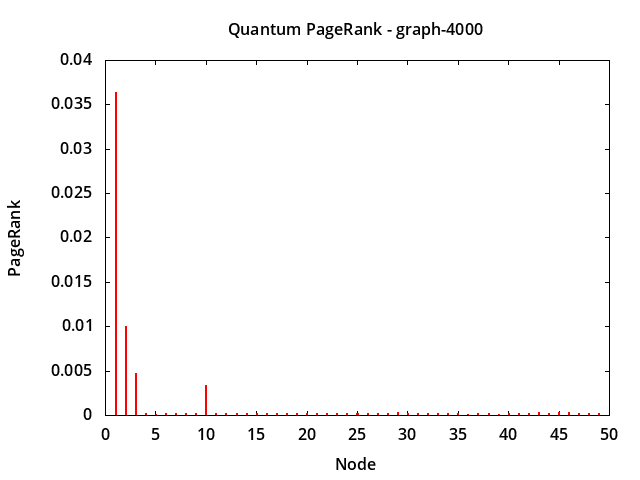Figure 4: 4000 Node Random Network Quantum PageRank Simulation

  Node  Classical  Node  Quantum
     1  0.016445      1  0.036373
     2  0.011036      2  0.009984
     3  0.007354      3  0.004696
    10  0.000755     10  0.003357
     4  0.000271      8  0.000244
     8  0.000249      4  0.000237
     9  0.000182      7  0.000219
     7  0.000170      6  0.000201
     6  0.000167      9  0.000187
     5  0.000146      5  0.000167

Table 3: 4000 Node Random Network Classical and Quantum PageRank, Nodes 1-10, Sorted by Rank, Time=100

[1] Quantum random walks: An introductory overview, J Kempe, Contemporary Physics, Volume 44, 2003, Issue 4.

[2] Quantum walks: a comprehensive review, Salvador Elías Venegas-Andraca, Quantum Information Processing, October 2012, volume 11, issue 5, pp 1015-1106.

[3] Exponential algorithmic speedup by a quantum walk, Andrew M. Childs, et. al., STOC'03, 2003, pp 59-68.

[4] Discrete-time quantum walk algorithm for ranking nodes on a network, Prateek Chawla, Roopesh Mangal, C. M. Chandrashekar, arXiv 1905.06575, 2019.

[5] Google in a Quantum Network, Paparo, G. D. and Martin-Delgado, M. A., Scientific Reports, 2012.

[6] Quantum Google in a Complex Network, Paparo, Giuseppe Davide, et. al., Scientific Reports, 2013.

[7] Quantum Google Algorithm: Construction and Application to Complex Networks, G.D. Paparo, et. al., arXiv 1409.3793, 2014.

[8] Quantum Speed-Up of Markov Chain Based Algorithms, Mario Szegedy, FOCS'04, 2004, pp 32-41.