Interference and Quantum Computations

R. Perry, 30 March 2018, QCE
Quantum computation of a function f(x) is generally described by a unitary transformation Uf such that:

Uf |x, y> = |x, y⊕f(x)>

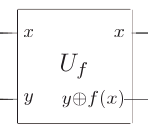
corresponding to the circuit diagram ([1], page 31):

These descriptions are correct if x,y ∈ {0,1}. But if x and/or y are superpositions then these descriptions may be misleading, and in particular the input x may not pass through Uf unchanged due to interference between the qubits.

Note that the ⊕ operation and function f(x) can only be applied directly to {0,1} operand values. For superpositions the operations are applied separately to each part.

In general we have:

Uf |x, y> = |Ψ>
 
  = |w, z>   if separable

Consider the CNOT operation, so f(x) = x and Uf performs y⊕x.

If |x> = |0> + |1> and |y> = |0> - |1> then (leaving out some factors of 1/sqrt(2)):

CNOT |x, y> = |0> (|0⊕0> - |1⊕0>) + |1> (|0⊕1> - |1⊕1>)
 
  = |0> (|0> - |1>) + |1> (|1> - |0>)
 
  = |0> (|0> - |1>) - |1> (|0> - |1>)
 
  = (|0> - |1>) (|0> - |1>)
 
  = |w, y>

So |x> is changed to |w> = |0> - |1> and y is unchanged.

In this case the action of operating on y with f(x) changes x and does not affect y.

This effect is due only to interference between the qubits. There is no entanglement as the result is separable into a product state.

For comparison, entanglement would occur using inputs |x> = |0> + |1> and |y> = |0>:

CNOT |x, y> = |0> |0⊕0> + |1> |0⊕1>
 
  = |0> |0> + |1> |1>

The state |00> + |11> is entangled and can not be factored into a product state.

From the viewpoint of a quantum computing simulation, x,y are indices into an array of amplitudes.

An amplitude table for |w,z> = CNOT |x,y> is constructed by setting w=x and z=x⊕y.

Leaving out some factors of 1/sqrt(2), the initialization |x> = |0> + |1> and |y> = |0> - |1> corresponds to:

(|0> + |1>) (|0> - |1>) = |00> - |01> + |10> - |11>

Letting a represent amplitude in the table, with input amplitudes q and output amplitudes r: 

                       CNOT: z = x⊕y

              x y   a  ->  x z   a  =   x y   a
     q[0]     0 0   1      0 0   1      0 0   1     r[0] = q[0]
     q[1]     0 1  -1      0 1  -1      0 1  -1     r[1] = q[1]
     q[2]     1 0   1      1 1   1  \/  1 0  -1     r[2] = q[3]
     q[3]     1 1  -1      1 0  -1  /\  1 1   1     r[3] = q[2]
Effectively, CNOT simply swaps the amplitudes of states |10> and |11>.

Although the table was constructed by explicitly replacing y with x⊕y, the result is the same as described above for interference, where x is changed and y is unchanged, which has amplitudes:

(|0> - |1>) (|0> - |1>) = |00> - |01> - |10> + |11>

For comparison, the amplitude table for entanglement, with initialization |x> = |0> + |1> and |y> = |0>, is: 

                       CNOT: z = x⊕y

              x y   a  ->  x z   a  =   x y   a
     q[0]     0 0   1      0 0   1      0 0   1     r[0] = q[0]
     q[1]     0 1   0      0 1   0      0 1   0     r[1] = q[1]
     q[2]     1 0   1      1 1   1  \/  1 0   0     r[2] = q[3]
     q[3]     1 1   0      1 0   0  /\  1 1   1     r[3] = q[2]
References

[1] Quantum Computation and Quantum Information, 10th Anniversary Edition, Michael A. Nielsen & Isaac L. Chuang, Cambridge University Press, 2010.