Single qubit operations are first illustrated for systems with 1, 2, and 3 qubits. Then a distributed approach is considered for a 6-qubit system with 8 processing nodes, which extends directly to the general case. Performance is evaluated by simulating the Bernstein & Vazirani quantum algorithm on a high-performance cluster of nodes. Multithreading on each node is also described and evaluated.
For a system with n qubits there are N=2n states
with amplitudes represented by q[0]...q[N-1].
A single qubit gate operation affects all of the amplitudes, in pairs.
For example, flipping the k'th qubit swaps amplitudes:
t = q[i]; q[i] = q[j]; q[j] = t;where indices
i and j differ only in the k'th bit:
the k'th bit of i is 0,
and the k'th bit of j is 1.
Performing a Hadamard transformation on the k'th qubit
updates each pair of amplitudes:
t0 = q[i]; t1 = q[j]; q[i] = (t0+t1)/√2; q[j] = (t0-t1)/√2;In the following the indices are listed in binary, grouped according to the pairs which are affected together.
If the system consists of a single qubit, then the only possible values for
indices i and j are 0 and 1:
0 q[0] 1 q[1]
For a 2-qubit system, operating on the last qubit:
x 0 0 q[0] 0 1 q[1] 1 0 q[2] 1 1 q[3]
x represents the value of the other qubit, so the pairs
can be described as (x 0) and (x 1) for
each value of x.
Operating on the first qubit,
the pairs are (0 x) and (1 x) for
each value of x:
x
0 0 q[0]
1 0 q[2]
0 1 q[1]
1 1 q[3]
For a 3-qubit system, operating on the last qubit,
the pairs are (x y 0) and (x y 1) for
each value of x and y:
x y 0 0 0 q[0] 0 0 1 q[1] 0 1 0 q[2] 0 1 1 q[3] 1 0 0 q[4] 1 0 1 q[5] 1 1 0 q[6] 1 1 1 q[7]
Operating on the middle qubit,
the pairs are (x 0 y) and (x 1 y):
x y 0 0 0 q[0] 0 1 0 q[2] 0 0 1 q[1] 0 1 1 q[3] 1 0 0 q[4] 1 1 0 q[6] 1 0 1 q[5] 1 1 1 q[7]
Operating on the first qubit,
the pairs are (0 x y) and (1 x y):
x y
0 0 0 q[0]
1 0 0 q[4]
0 0 1 q[1]
1 0 1 q[5]
0 1 0 q[2]
1 1 0 q[6]
0 1 1 q[3]
1 1 1 q[7]
If the number of qubits is so large that the array of amplitudes will not fit in memory on a single processing node, then a distributed approach can be used. This will be illustrated using a 6-qubit system, with the array of amplitudes distributed over 8 nodes, so the first 3 bits of the amplitude index can specify the node on which the value is stored.
Program states.c was used to generate tables similar to those
shown above listing the amplitude pairs involved in
operations on the k'th qubit.
See states-n-k.txt:
states-6-0.txt,
states-6-1.txt,
states-6-2.txt,
states-6-3.txt,
states-6-4.txt,
states-6-5.txt.
Operations on qubits 0 to 2 can be performed on each processing node independently, as can be seen for example in this reformatted version of states-6-0.txt for operations on qubit 0:
0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 0 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 0 1 1 0 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 0 1 0 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 0 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 1 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 1 0 0 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 0 1 0 0 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1Each block of bits corresponds to amplitudes which are stored on a single node, with the node number specified by the first 3 bits of the index.
Operations on qubits 3 to 5 can not be performed independently on each node, as can be seen for example for operations on qubit 3 (states-6-3.txt):
0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 0 1 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 0 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 0 1 1 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 1 0 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 0 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1In this case each block of bits corresponds to amplitudes which are stored on a pair of nodes: nodes 0,1 for the first block, 2,3 for the second block, etc.
For operations on qubit 5 (states-6-5.txt) the pairs of nodes are: nodes 0,4 for the first block, 1,5 for the second block, etc.:
0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 1 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 1 1 1 1 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1
In the general case
for a system with n qubits,
the top p bits of the amplitude index
can specify one of P=2p processing nodes, and each
node stores M=2m amplitudes, where
m=n-p.
Operations on qubits 0 to m-1 can be performed
on each processing node independently in parallel,
which represents a computational speedup by a factor of P.
Operations on qubits m to n-1 require
communication between pairs of processors, so although there is
a computational speedup by a factor of P for the nodes
operating in parallel, the communication overhead may negate that gain,
and overall processing could be slower than using a single node.
The distributed system can simulate
more qubits than can fit in memory on a single processing node,
but unless the number of nodes is very large this gain may not be significant.
For example, simulating 32 qubits requires an array of 232
amplitudes, and using 16-byte double-precision complex values, that
is a total of 64 GB of memory.
Using 256 nodes, each of which has at least 64 GB of memory
(total memory 16 TB), 8 more qubits can be simulated,
for a total of 40 qubits.
That is only a 25% gain in number of qubits for a factor of 256 increase
in resources used.
The number of additional qubits which
can be simulated using P processing nodes is log2(P),
so each doubling of resources yields a gain of only 1 more qubit.
Program BV.c from QCE will be used to evaluate the performance of single qubit operations in a distributed environment. It simulates the Bernstein & Vazirani quantum algorithm which determines the hidden bit string of a parity function, and mainly performs Hadamard transformations.
BV.c uses MPI (Message Passing Interface) for distributed communication, and for the results reported here it was linked with version 3.0.2 of Open MPI and run on an InfiniBand network of processing nodes, each with 16 3.2 GHz cores and 128 GB RAM.
An array of size C=2c
was used as a cache for data transferred between nodes.
Run-time measurements indicate that
performance improves up to c=11; beyond that
there is not much further improvement for this application and environment:
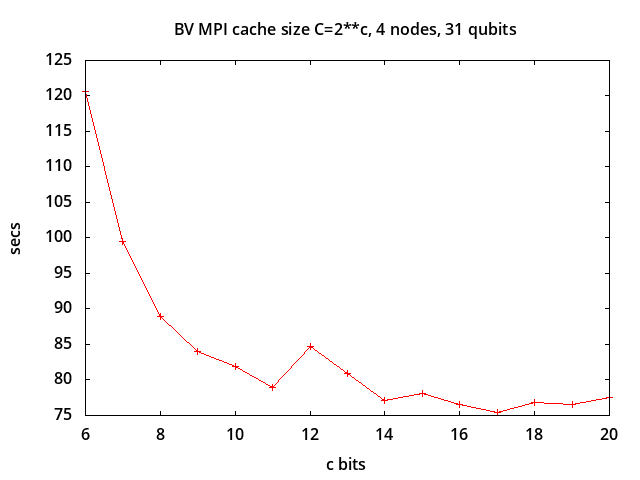
Run-time vs. Cache Size: 4 Nodes, 31 Qubits |
n
c 21 25 29 31 32 33
9 0.88 1.91 20.45 83.97 172.78 353.48
10 0.87 1.89 19.74 81.84 167.23 344.78
11 0.87 1.81 19.00 78.89 161.62 333.40
12 1.02 2.09 21.09 84.65 172.29 357.20
13 1.05 2.02 20.07 80.86 163.85 344.21
n Qubits
|
Some tests using the MPICH (3.2.1) and Intel (2019 Update 3) implementations of MPI were performed:
c MPICH Intel OpenMPI
7 2437.09 105.13 99.48
9 781.21 91.29 83.97
11 472.62 90.35 78.89
13 464.33 86.49 80.86
15 382.91 82.10 78.15
Run-time in Seconds: 4 Nodes, 31 Qubits
Since Open MPI had the best performance no further testing of alternatives was considered.
For subsequent performance measurements Open MPI with c=11 is used,
so the cache size is C=211=2048 elements
(16-byte double complex values) for a total of 32768 bytes.
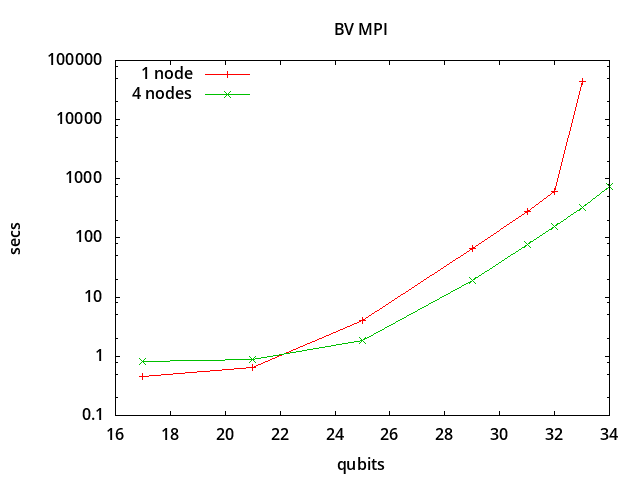
Starting around
n=25 qubits, distributed processing using 4 nodes
shows a performance improvement over single node processing,
approaching a factor of 4 speedup as the number of qubits is increased:
Run-time vs. Number of Qubits |
secs speedup
n 1 node 4 nodes ratio
17 0.46 0.82 0.56
21 0.65 0.88 0.74
25 4.03 1.82 2.21
29 67.08 19.16 3.50
31 285.76 77.77 3.67
32 615.60 158.79 3.88
33 43832.15 332.56 131.80
34 ---- 736.54 ----
|
For n=33 qubits, 128 GB of memory is required
just for the array of quantum amplitudes. On a single 128 GB node
this causes swapping, and the run-time increases to 43832 seconds
(about 12 hours) which is a factor of 36 times what would
be expected following the exponential scaling (20 minutes).
For n=34 qubits a single node has insufficient
memory and can not perform the simulation.
In the general case for a system with M=2m amplitudes
stored on a single processing node, t bits of the
amplitude index can specify one of T=2t parallel
threads on the node.
Operations on any qubit can be performed by each thread independently,
which could represent a computational speedup by a factor of T
if the node has T cores.
However the actual speedup may be limited by memory bandwidth.
Let b=m-t represent a number of low-order bits of the amplitude index.
For operations on qubits 0 to b-1, computations can be
assigned to threads in blocks directly using the top t bits
as the thread number similar to operations on qubits 0 to m-1
in a distributed environment. For example, the top 3 bits in the
states-6-0 table can interpreted as a thread number
for processing a block of amplitudes in 8 threads.
For operations on qubits b to m-1,
communication between pairs of threads can be avoided
by constructing the thread number from
t-1 of the top t bits of the
amplitude index, together with bit b-1.
For example, the top 2 bits together with bit 2 from the
states-6-3 table can interpreted as a thread number
for operations on qubit 3 in blocks of amplitudes using 8 threads:
0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 0 1 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 0 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 0 1 1 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 1 0 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 0 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1In this case the top 4 blocks correspond to threads 000, 010, 100, 110 (0,2,4,6) and the bottom 4 blocks to threads 001, 011, 101, 111 (1, 3, 5, 7).
Similarly, for operations on qubit 4, bits 5,3 together with bit 2 can represent the thread number (reformatted states-6-4.txt):
0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 1 0 0 0 0 1 1 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 1 1 0 0 0 1 1 1 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 1 0 0 0 1 1 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 1 0 0 1 1 1 1 1 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 1 0 0 1 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 1 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 0 1 0 0 1 1 0 1 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 1 1 1 0 0 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1For operations on qubit 5, the thread number can be represented by bits 4,3 together with bit 2 from the states-6-5 table:
0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 1 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 1 1 1 1 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1Let
d=k-b represent a number of low-order bits
from thread number ID.
For operations on qubit k, with k≥b, the general
bit layout for the amplitude indices is:
<------------------------------- m ----------------------------------->
<------ t-d-1 ----------><- 1 -><----- d ------><--- 1 ----><-- b-1 -->
top (t-d-1) bits from ID, bit k, d bits from ID, bit 0 of ID, 2b-1
^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^
one of the indicated pieces could be empty depending on k
If k=m-1 then t-d-1=0 and all of the thread ID
bits occur to the right of bit k.
If k=b then d=0 and t-1 of the thread ID
bits occur to the left of bit k.
Together with bit k,
the least-significant b-1 bits specify the
2b-1 pairs of amplitude indices
processed by each thread.
states.c
compiled with the -fopenmp option
can be used to check the amplitude pairs processed by each thread
using OpenMP.
Compiled with BAD defined, linear start,stop thread assignment is used,
and half of the threads perform no work when k≥b.
Otherwise the thread assignment described above is used and each thread
performs the same number of iterations.
Examples using n=6,k=5 are shown in
states-6-5-omp.txt.
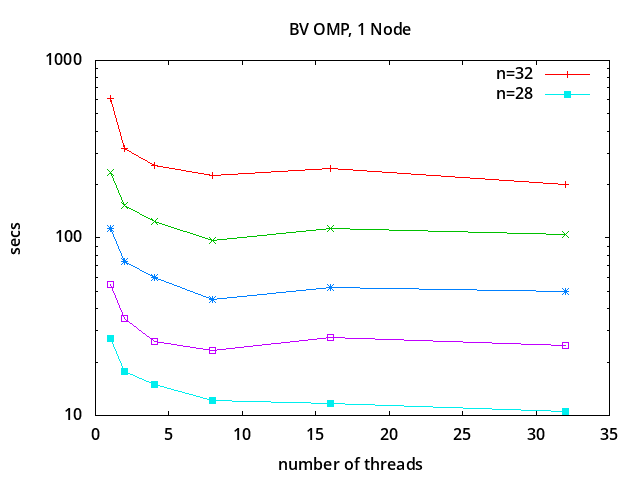
The following results were obtained using a single processing node with 16 cores (2 sockets with 8 cores per socket, Intel Xeon Gold 6134 @ 3.20GHz) and 96 GB RAM:
Run-time vs. Number of Threads |
number of threads
n 1 2 4 8 16 32
32 611.11 319.05 255.64 224.63 247.65 199.00
31 235.11 153.29 124.02 96.66 113.37 104.51
30 113.84 73.70 60.03 45.07 52.76 49.98
29 55.05 35.30 26.28 23.18 27.67 24.65
28 27.00 17.66 14.90 12.11 11.74 10.54
n Qubits on a Single Node
|
Compared to using a single thread, performance improves significantly with 2 threads and 4 threads, but does not improve much beyond that as the number of threads is increased further. This indicates that the computations are limited by memory access bandwidth.
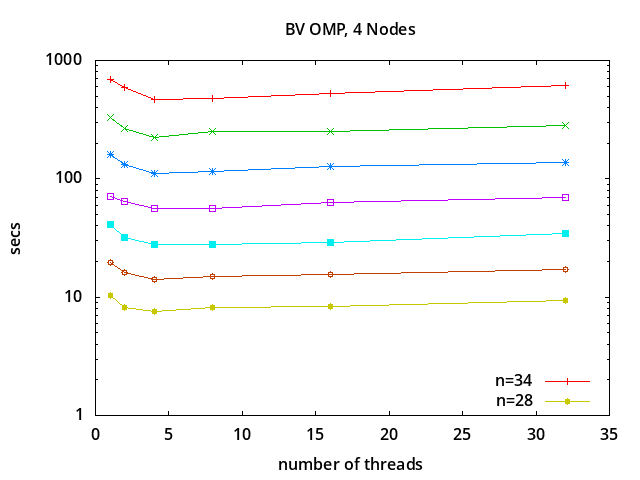
Results using OpenMP together with MPI on 4 processing nodes also show speedup with 2 and 4 threads, and not much improvement beyond that:
Run-time vs. Number of Threads |
number of threads
n 1 2 4 8 16 32
34 692.86 587.13 467.99 474.97 521.16 614.83
33 330.98 266.77 225.29 249.01 252.61 283.80
32 161.67 132.37 111.55 115.44 127.93 138.75
31 71.58 64.11 56.01 55.88 62.64 69.00
30 40.79 32.04 27.71 27.60 28.74 34.48
29 19.64 16.04 14.20 14.89 15.48 17.17
28 10.42 8.21 7.55 8.11 8.36 9.35
n Qubits on 4 Nodes
|