Magnetic Pulse Error Analysis

R. Perry, 5 June 2018, QCE
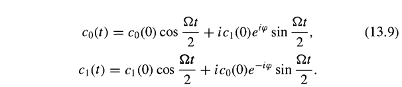
The wave function for a proton spin acted on by a resonant magnetic pulse (ω=ω0) with phase shift φ is derived in chapters 12 and 13 of [1]:



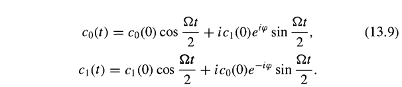
Here we assume that ω is not necessarily equal to ω0, and we derive the formulas: 

  c0(t) = c0(0)(cos(dt)-(ia/d)sin(dt)) + mc1(0)(ib/d)eipsin(dt)

  c1(t) = mc1(0)(cos(dt)+(ia/d)sin(dt)) + c0(0)(ib/d)e-ipsin(dt)

where p=φ, a=(ω-ω0)/2, b=Ω/2, and d=sqrt(a2+b2). The multiplier m of c1(0) is m=1 for a simple π-pulse, and m=-1 for pulses implementing the Hadamard transformation (called Aj transformation in [1]). The derivation is shown below after the analysis results.

Results

In each of the plots shown, the midpoint of the horizontal axis corresponds to no error, so points to the left and right of center represent the effects of negative and positive errors respectively.

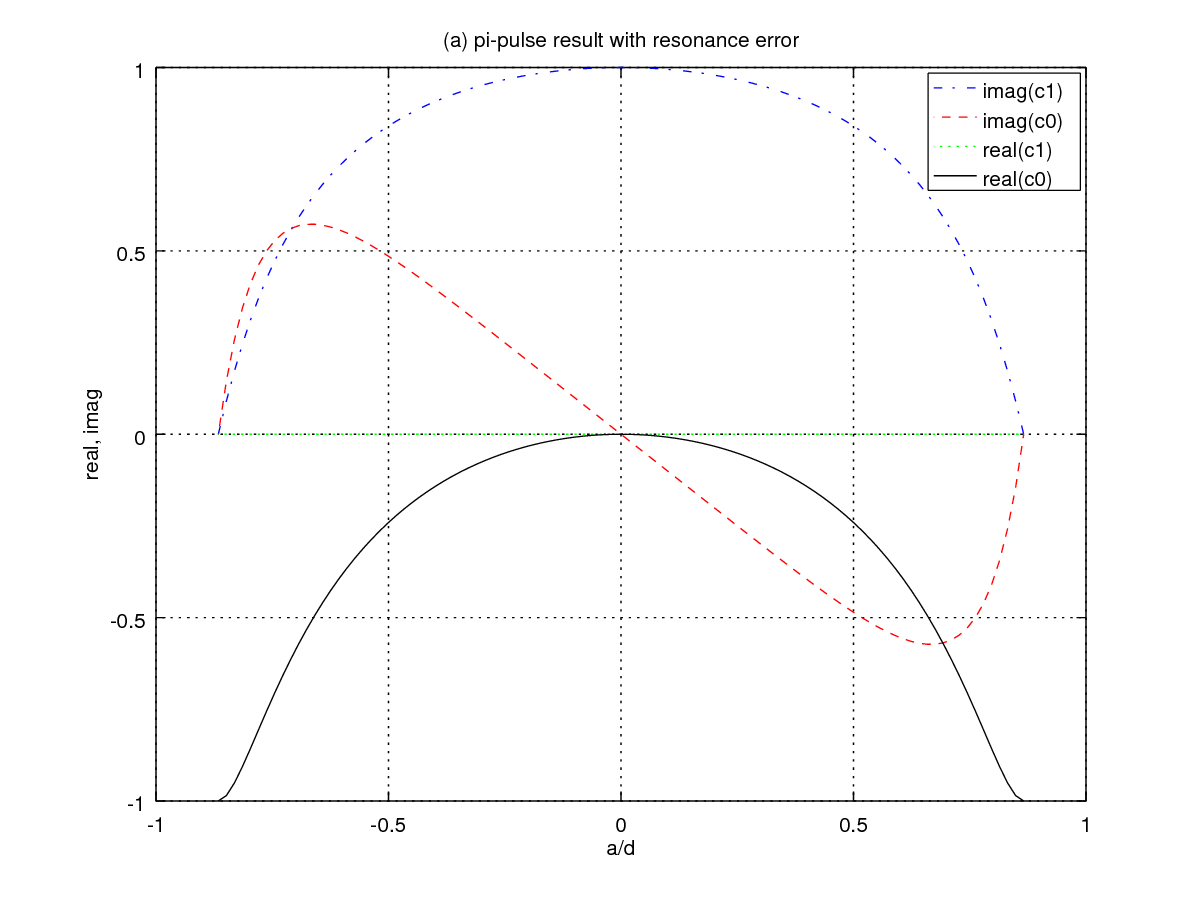
Figure (a) shows c0(t1) and c1(t1) for a non-resonant π-pulse (m=1,p=0) applied until time t1=π/Ω=π/(2b): 
  c0(t1) = c0(0)(cos(A)-irasin(A)) + c1(0)(irbsin(A)) ==>> cos(A)-irasin(A)
  c1(t1) = c1(0)(cos(A)+irasin(A)) + c0(0)(irbsin(A)) ==>> irbsin(A)
with ra=a/d, rb=b/d, and A=π/(2rb). The initial conditions are c0(0)=1,c1(0)=0, and with no error we should have c0=0,c1=i at time t1.

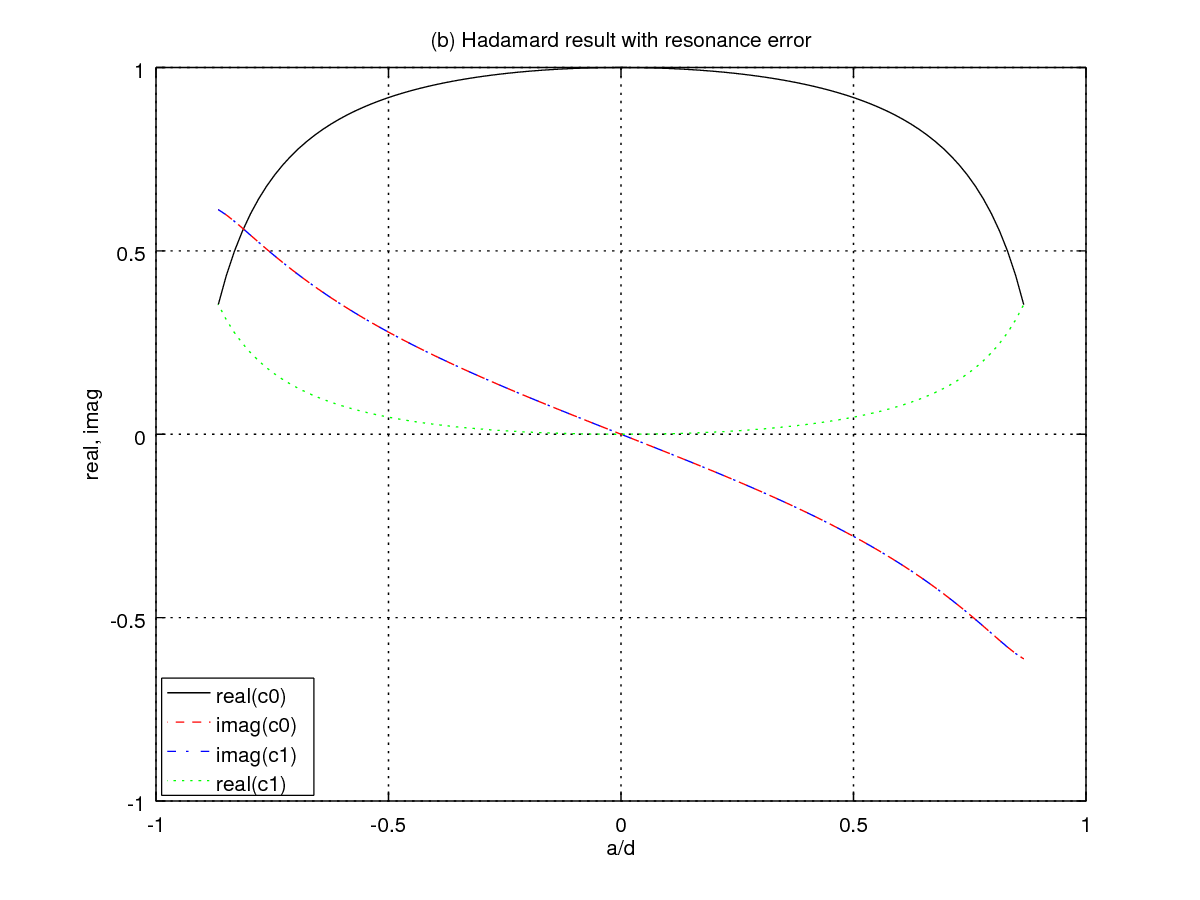
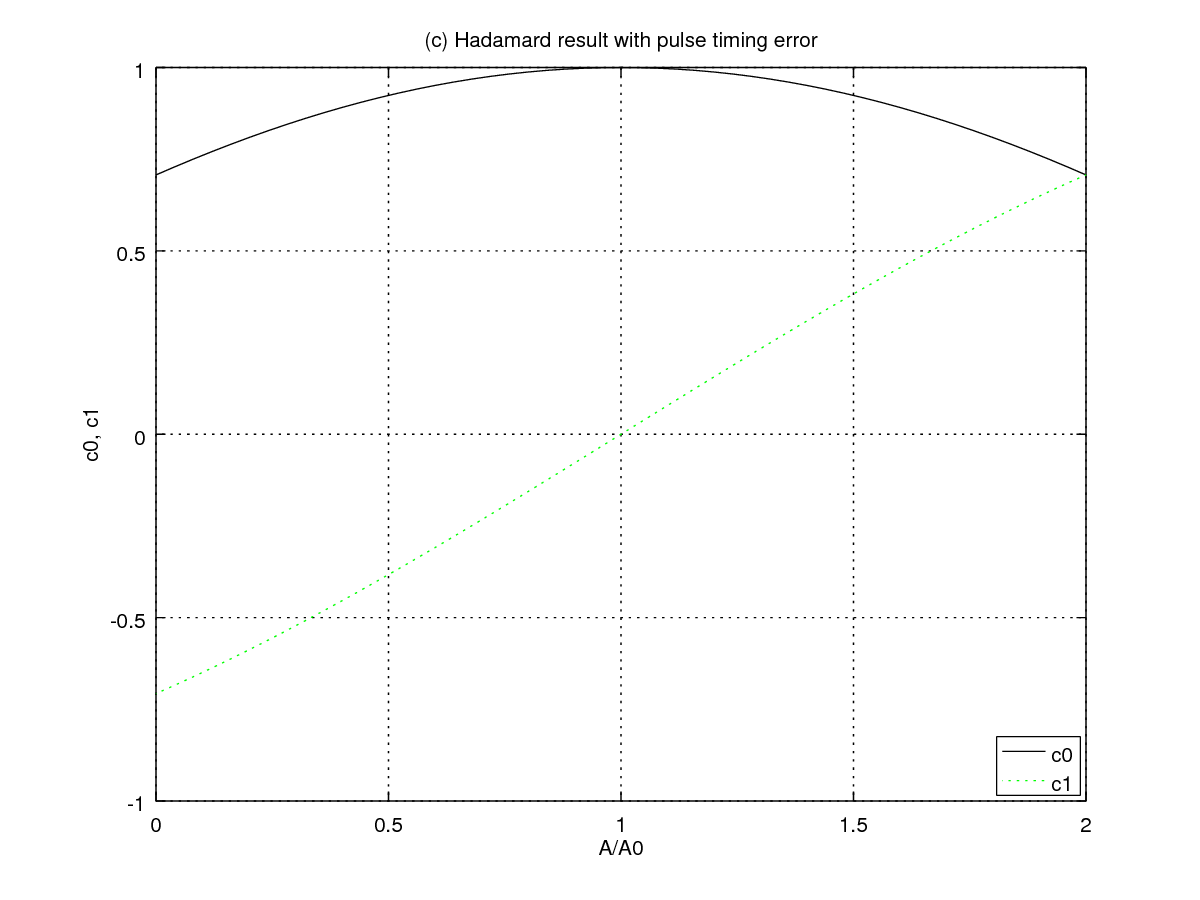
Figures (b,c) show results for a Hadamard transformation (m=-1,p=π/2): 

  c0(t) = c0(0)( cos(A)-irasin(A)) + c1(0)(rbsin(A))
  c1(t) = c1(0)(-cos(A)-irasin(A)) + c0(0)(rbsin(A))
With initial conditions c0(0)=c1(0)=1/sqrt(2) and no error (A=π/4) we should have c0=1,c1=0 at the end of the pulse.

For Figure (b) the non-resonant pulse is applied until time t2=π/(2Ω)=π/(4b): 

  c0(t2) = ( cos(A)-irasin(A)+rbsin(A))/sqrt(2)
  c1(t2) = (-cos(A)-irasin(A)+rbsin(A))/sqrt(2)
with A=π/(4rb).

For Figure (c) the pulse is resonant (a=0,b=d) and applied until time t, but there is a timing error: 

  c0(t) = ( cos(A)+sin(A))/sqrt(2)
  c1(t) = (-cos(A)+sin(A))/sqrt(2)
With no timing error we would have A=A0=dt=π/4.

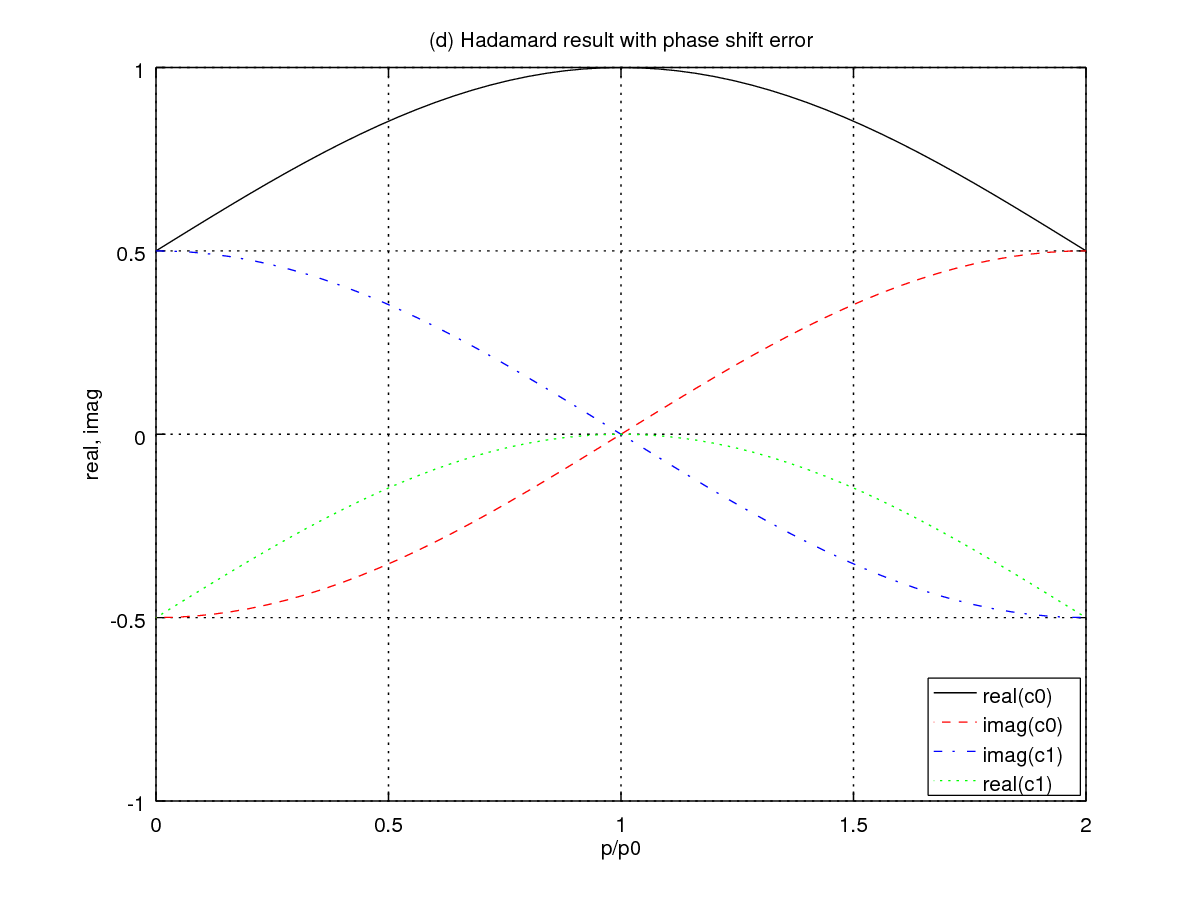
For Figure (d) the pulse is resonant and applied for the correct time, but there is a phase shift error: 

  c0(t2) =  c0(0)cos(A) - c1(0)ieipsin(A)  ==>> (sin(p)+1-i*cos(p))/2
  c1(t2) = -c1(0)cos(A) + c0(0)ie-ipsin(A) ==>> (sin(p)-1+i*cos(p))/2
With no phase shift error we would have p=p0=π/2

Derivation

The Hamiltonian for the proton spin in a uniform magnetic field is given in [1]:


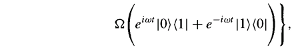
Including the phase shift φ the last term becomes [1]:

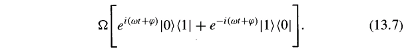
Letting Ψ(t) = g0|0> + g1|1> and substituting into the Schrödinger equation (12.1) we obtain: 

  i ∂g0/∂t = -(ω0 g0 + Ω g1 ei(wt+φ))/2

  i ∂g1/∂t = -(-ω0 g1 + Ω g0 e-i(wt+φ))/2
Now perform the substitutions: 
  g0 = c0 eiωt/2,  ∂g0/∂t = (∂c0/∂t) eiωt/2 + (iω/2) c0 eiωt/2

  g1 = c1 e-iωt/2,  ∂g1/∂t = (∂c1/∂t) e-iωt/2 - (iω/2) c1 e-iωt/2
which yield: 
  i ∂c0/∂t = c0 (ω-ω0)/2 - c1 (Ω/2) eiφ

  i ∂c1/∂t = -c1 (ω-ω0)/2 - c0 (Ω/2) e-iφ

Letting a=(ω-ω0)/2 and b=Ω/2, and writing in matrix form:

∂c0/∂t
∂c1/∂t
  =  
-ia   ibeiφ
ibe-iφ   ia
   
c0
c1
  = A c
the solution is: 
  c(t) = eAt c(0) = V eΛt V-1 c(0)
where eΛt=diag(eidt,e-idt), the eigenvalues of A are ±id, d=sqrt(a2+b2), and the columns of V are the eigenvectors:
V =  
beiφ   beiφ
a+d   a-d

Substituting and simplifying we obtain:

c(t) =  
cos(dt)-(ia/d)sin(dt)   (ib/d)eipsin(dt)
(ib/d)e-ipsin(dt)   cos(dt)+(ia/d)sin(dt)
   
c0(0)
c1(0)
References

[1] Introduction to Quantum Computers, Gennady P Berman, Gary D Doolen, Ronnie Mainieri, Vladimir I Tsifrinovich, World Scientific, 1998.