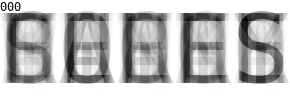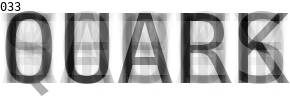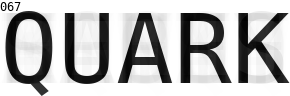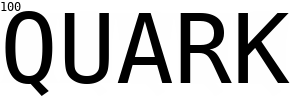
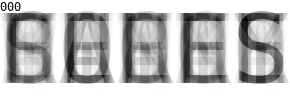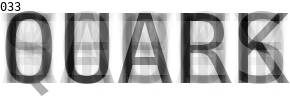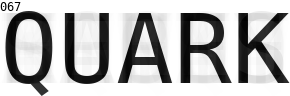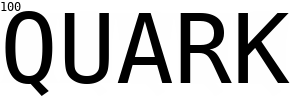
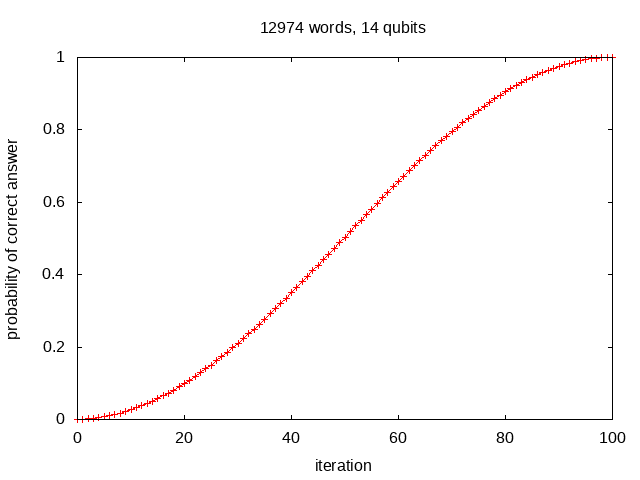
Quantum computing simulation is used to solve a Wordle puzzle. Guesses are displayed as a superposition of possible words with intensity weighted by their measurement probability. Using Grover's algorithm the correct answer is found with probability 1 after 100 iterations.
(shift-reload to re-run animated gifs)
Wordle [1] is a guessing game using 5-letter words. The New York Times version [2] is written in Javascript [3] from which the lists of answers and other allowed guesses were extracted and converted to C++ code words.h and words.cc. For visualization, pgm.h and pgm.cc encode text versions of Portable Gray Map images for characters A-Z and 0-9 (a-z.png and 0-9.png) which were created in gimp using a monospace font.
The main program main.cc uses the
QCE quantum simulation library
and performs Grover's search algorithm [4,5].
Starting with a superposition of all possible words (12974 ~= 214 words),
it creates PGM images with the grayscale intensity of each word
scaled by its measurement probability.
The correct answer appears with probability ~= 1 after
(π/4)*sqrt(214) ~= 100 iterations.
There is an option to find each letter separately (sequentially),
using 5 qubits to represent the 26 letters,
which takes only (π/4)*sqrt(25) ~= 4 iterations per letter.
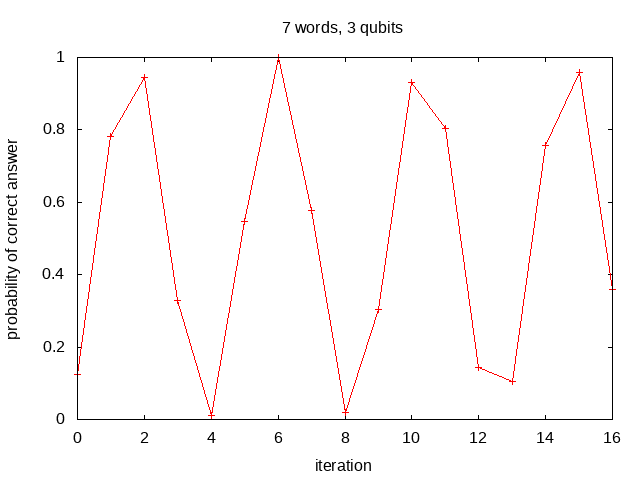
There is also an option to run using a smaller set of just 7 words for debugging.
Program text output for the QUARK example above is shown in wordle.txt. For each iteration it displays the probability, one minus the probability, and index number of the correct solution, followed by the probability, one minus the probability, index number and word for the two most likely measurements. The script gif.sh was used to combine the PGM image outputs into an animated GIF.
Examples - QUARK, txt, plot - SUSHI, txt - small, txt, debug, plot
Sequential Example: QUARK, txt
Quantum wordle requires a quantum oracle to check the superposition of words, thus it can not be used to play the standard/classical wordle game such as that from the New York Times. Furthermore, only information about words being correct or incorrect is used; other clues provided by classical wordle, such as letters being correct but in the wrong position, are not used since there does not seem to be any way to incorporate that into the quantum search algorithm. And although finding each letter separately is faster than checking for all words in parallel, that is not consistent with the normal way of playing wordle.
Since the number of words (M=12974) is less than the number of quantum states
(N=16384=214),
there are many states which do not correspond to any word.
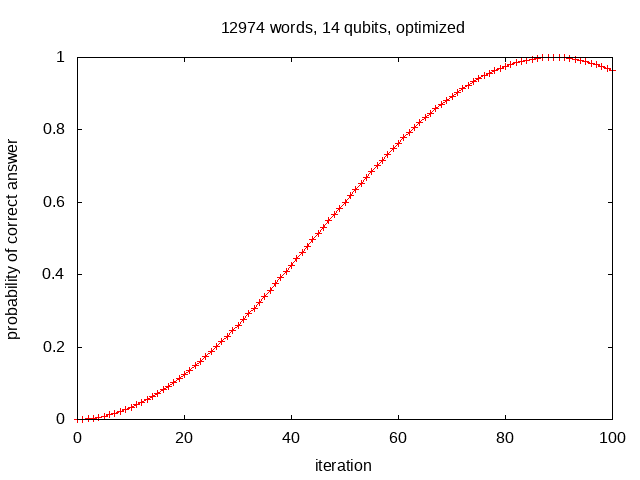
The search efficiency can be improved by initializing the infeasible states to
zero amplitude, and using M instead of N throughout the simulation.
This reduces the number of iterations from 100 (txt)
to (π/4)*sqrt(12974) ~= 89 (txt):
 |
 |
The theoretical exact number of iterations required for Grover's algorithm to provide
the correct answer with probability 1 is:
k=(π/2)/θ-1/2 where θ=2*sin-1(a)
and a=1/sqrt(N).
This is generally not an integer, so it must be rounded up or down to the nearest integer.
For example, with N=16384 the optimal number of iterations is 100.03
and with N=8 the optimal number is 1.6734.
When the required number of iterations is on the order of 100 or more, the probability peak is rather flat, so the exact number of iterations used does not make any significant difference. But for smaller problems the probability may not be near 1 for any integer number of iterations, and it can also be very sensitive to the number of iterations.
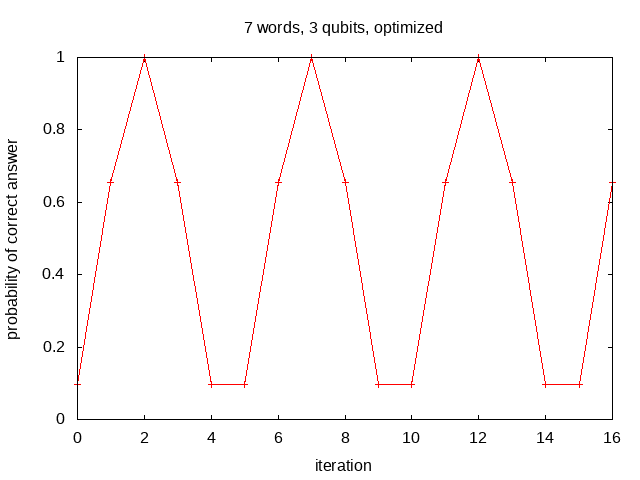
For small problems which also have at least one infeasible state,
we can start with a desired integer number of iterations and
solve for the required rotation angle θ.
The M feasible states can be initialized to amplitude
a=sin(θ/2) and one infeasible state initialized to amplitude
b=sqrt(1-M*a2).
Using the small set of 7 words this technique achieves a success probability of 1
(within the machine precision) after 2 iterations (txt)
compared to the unoptimized solution probability 0.945312
(txt):
 |
 |
[1] Wordle, Wikipedia, https://en.wikipedia.org/wiki/Wordle
[2] New York Times Wordle, https://www.nytimes.com/games/wordle/index.html
[3] New York Times Wordle Javascript source code, https://www.nytimes.com/games/wordle/main.9622bc55.js (local)
[4] Grover's algorithm, Wikipedia, https://en.wikipedia.org/wiki/Grover's_algorithm
[5] Quantum Mechanics Helps in Searching for a Needle in a Haystack, Lov K. Grover, Physical Review Letters, Vol. 79, No. 2, July 1997, pp. 325-328, https://arxiv.org/abs/quant-ph/9706033
Some related projects: Qwordle, uses two "entangled" answers; Quantle, guess quantum computing equation instead of a word; another Qwordle, based on Grover's algorithm, finds one letter at a time (news article); the mathematically optimal first guess in Wordle; solving Wordle using information theory.