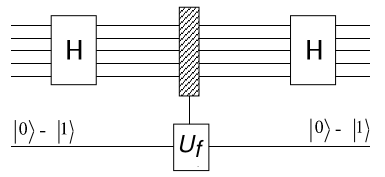
Figure 4. Network representation of Bernstein-Vazirani's algorithm
Write a C program to compare classical and quantum computing solutions to the problem of determining the n-bit coefficient hidden inside a Boolean function (Bernstein & Vazirani problem [1]). This problem demonstrates the speedup possible with a quantum computer, and it has been extended to practical applications such as database searching and breaking cryptography. For background on quantum computing see [2]. For some recent news see [3].
The Boolean function is the bitwise dot product f(x) = a•x = a0x0 ⊕ a1x1 ⊕ ... ⊕ an-1xn-1 where a is the hidden coefficient. ai and xi are bit i of a and x, and ⊕ means XOR. In other words f(x) is the modulo-2 sum of the bits in the bit-wise AND (a & x). a and x can also be written as sums of powers of 2: a = ∑ ai 2i, x = ∑ xi 2i, where each ai and xi is 0 or 1.
You cannot look inside the function to see a, however you can call the function and see the return value for any input. A classical solution must invoke f() n times to determine the hidden coefficient: one call for each bit of a, using powers of 2 for the x values. But the quantum computing solution to this problem can determine the hidden coefficient with just one function call, regardless of the size of n. If we had a physical quantum computer we could set it up using n+1 qubits to do this, with n qubits representing the input values and the extra qubit for the function value [1, Figure 4].
Simulating the quantum computations on a classical computer requires an array of size 2n+1 and is not efficient, but can demonstrate the effectiveness of the quantum algorithm. The array elements represent complex amplitudes of the quantum states, and the magnitude squared of an amplitude corresponds to the probability of measuring that state.
Simulation Library
The following routines are declared in qc.h and defined in qc.c:
// the hidden coefficient (for debugging) // unsigned long A( unsigned long N); // the classical Boolean function // unsigned int fx( unsigned long x, unsigned long N); // 0 <= x <= N-1 // the quantum Boolean function // void fq( double _Complex q[], unsigned long M); // q[0]...q[M-1] // perform Hadamard transformation on all qubits // void H( double _Complex q[], unsigned long M);
qc.h and qc.c are available in
VECR a2/ and are used by the Makefile there.
To access these routines use: #include "qc.h"
Note that the hidden coefficient is randomly generated each time your program is run. For debugging you can access the coefficient by calling A(N).
The Hadamard transformation can be used to put qubits in a superposition of states and is one of the keys to the power of quantum computing. Each qubit can act like a 0 and 1 at the same time, so m qubits can represent the possible 2m values all at once.
Simulation Steps
srand(time(0));
Display a table of x and the function values.
Write functions to initialize the array and print the array.
Use something like the following code fragment to perform the quantum algorithm:
double complex q[M]; init(q,M); print(q,M); H(q,M); print(q,M); fq(q,M); print(q,M); H(q,M); print(q,M);Note that there is no loop in the quantum algorithm and fq() is only invoked once.
In a physical quantum computer we can not see the amplitudes, and a measurement collapses the state to a value based on probability (magnitude squared of amplitude). In a simulation we could simulate measurements, but it is often more useful to work with the amplitudes directly.
Start with a copy of your program from part 1 and modify it to include dephasing noise after calling fq(), something like this:
double complex q[M]; init(q,M); H(q,M); fq(q,M); R(q,M,phi); H(q,M);where you must implement R() to perform the Rφ transformation on all qubits:
| Rφ = |
|
The action of Rφ is: Rφ |0> = |0>, Rφ |1> = ejφ|1>
In step 3, instead of using scanf() to read from standard input, set n=8 and get an angle in degrees from the command-line, for example:
int main( int argc, char *argv[])
{
double ang = 0; if( argc > 1) ang = atof(argv[1]);
...
The only output must be a table with two columns of values suitable for plotting: i and |qi|2 (state probabilities), i = 0 ... M-1.
Results should show that with no noise (ang=0) as in part 1, the probability of measuring the correct value of the hidden coefficient is 1. But as ang increases this probability decreases and for ang=90 all possible measurement values are equally likely.
[1] Quantum algorithms revisited, R. Cleve, A. Ekert, C. Macchiavello, M. Mosca, Proc. R. Soc. Lond. A (1998) 454, 339-354. Recommended: sections 1-3. Excerpt:

Figure 4. Network representation of Bernstein-Vazirani's algorithm
[2] An Introduction to Quantum Computing, Without the Physics, Giacomo Nannicini, Nov 2018. Recommended: sections 1-3; skip example 4 and the proofs.
[3] Quantum leap, Don Monroe, CACM Jan. 2019. A new proof supports a 25-year-old claim of the unique power of quantum computing.