1. Binary Tree Basics
-
In a list, each node has up to one successor.
In a binary tree, each node has up to two children, known as a left child and a right child.
"Binary" means two, referring to the two children.
-
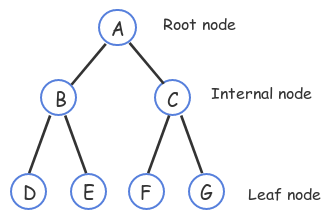
2. Binary Tree Definitions
- Leaf: A tree node with no children.
- Internal node: A node with at least one child.
- Parent: A node with a child is said to be that child's parent.
- A node's ancestors include the node's parent, the parent's parent, etc., up to the tree's root.
- Root: The one tree node with no parent (the "top" node).
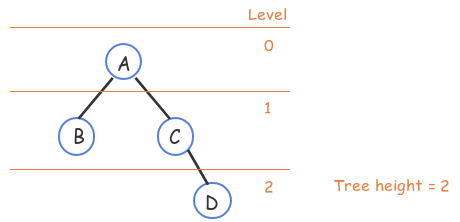
3. Depth, level, and height
- The link from a node to a child is called an edge.
- A node's depth is the number of edges on the path from the root to the node.
The root node thus has depth 0. - All nodes with the same depth form a tree level.
- A tree's height is the largest depth of any node. A tree with just one node has height 0.
- A tree is balanced if for any node, the heights of the node's left and right subtrees differ by only 0 or 1.
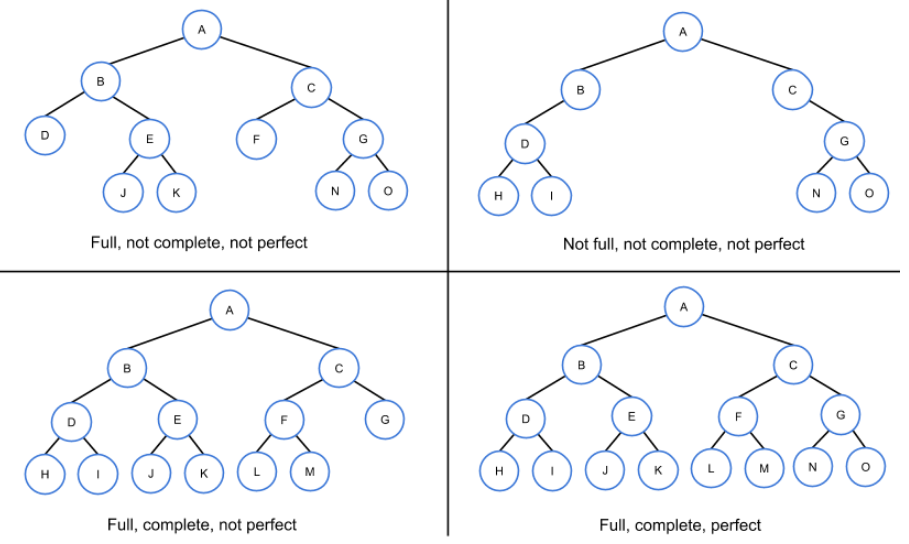
4. Special Types of Binary Trees
- A binary tree is full if every node contains 0 or 2 children.
- A binary tree is complete if all levels, except possibly the last level, are completely full and all nodes in the last level are as far left as possible.
- A binary tree is perfect, if all internal nodes have 2 children and all leaf nodes are at the same level.
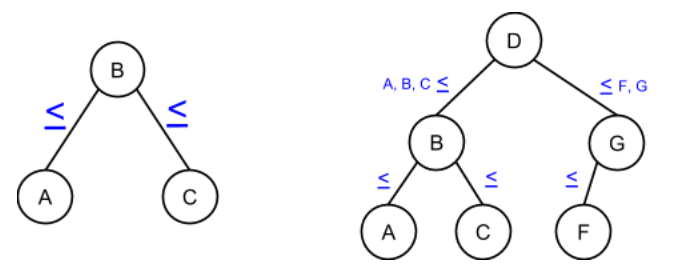
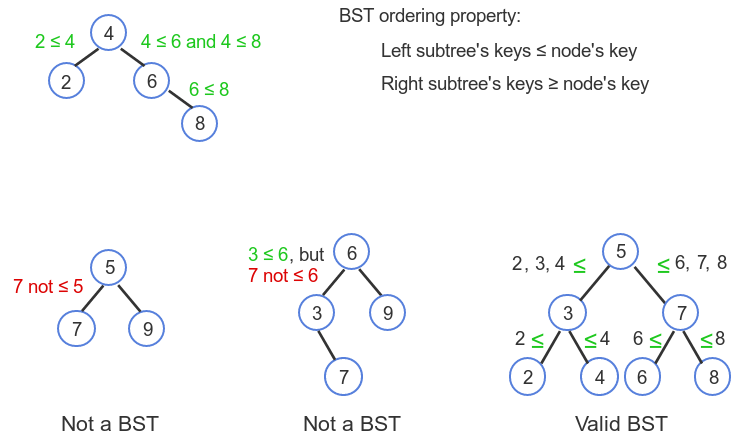
5. Binary Search Trees
-
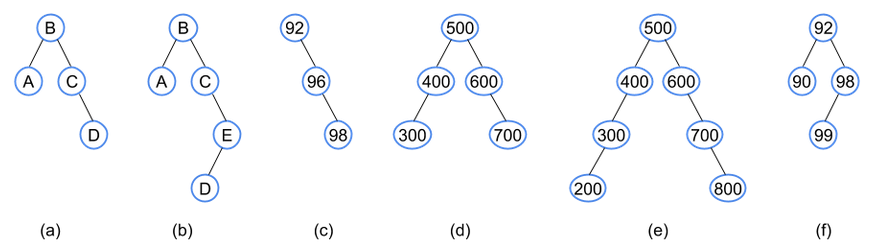
An especially useful form of binary tree is a binary search tree (BST),
which has an ordering property that any node's left subtree keys ≤
the node's key, and the right subtree's keys ≥ the node's key, which
enables fast searching for an item.
-
6. BST Examples
7. Balanced Trees
-
A tree is balanced if for any node, the heights of the node's left
and right subtrees differ by only 0 or 1.
8. BST Height
-
A tree's height
his the maximum number of edges from the root to any leaf.BST search time is
O(h).The minimum
N-node binary tree height ish = ⌊log2(N)⌋- achieved when each level is full except possibly the last.
The maximum
N-node binary tree height isN-1(the -1 is because the root is at height 0).-
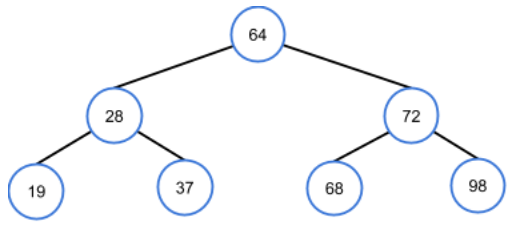
Perfect BST with minimum possible height for 7 nodes
9. Tree Traversal - Inorder, Preorder, Postorder
-

Mirror image traversals: reverse Left/Right order
10. Tree Framework
-
Tree/ or Tree.cc:
class Tree { private: Node *root; public: Tree() { root = nullptr; } void insert( long d); void print() const; };
11. Tree Node
-
Tree/ or Tree.cc:
class Node { friend class Tree; // so Tree can access the private data private: long data; Node *left, *right; public: // need constructor };