1. Insertion Sort
-
z8.3-insertionsort.cc
Insertion sort is a sorting algorithm that treats the input as two parts, a sorted part and an unsorted part, and repeatedly inserts the next value from the unsorted part into the correct location in the sorted part.
for (i = 1; i < numbersSize; ++i) { j = i; // Insert numbers[i] into sorted part // stopping once numbers[i] in correct position while (j > 0 && numbers[j] < numbers[j - 1]) { // Swap numbers[j] and numbers[j - 1] temp = numbers[j]; numbers[j] = numbers[j - 1]; numbers[j - 1] = temp; --j; } }
Initially, the first element (i.e., element at index 0) is assumed to be sorted, so the outer for loop initializes i to 1.
The inner while loop inserts the current element into the sorted part by repeatedly swapping the current element with the elements in the sorted part that are larger.
Once a smaller or equal element is found in sorted part, the current element has been inserted in the correct location and the while loop terminates.
2. Insertion Sort Complexity
-
Insertion sort's typical runtime is O(N2).
-
If a list has N elements, the outer loop executes N-1 times.
For each outer loop execution, the inner loop may need to examine all elements in the sorted part. Thus, the inner loop executes on average N/2 times.
So the total number of comparisons is proportional to (N-1)*(N/2), or O(N2).
- Other sorting algorithms involve more complex algorithms but faster execution.
-
If a list has N elements, the outer loop executes N-1 times.
3. Merge Sort
-
z8.4-mergesort.cc - pseudo-code
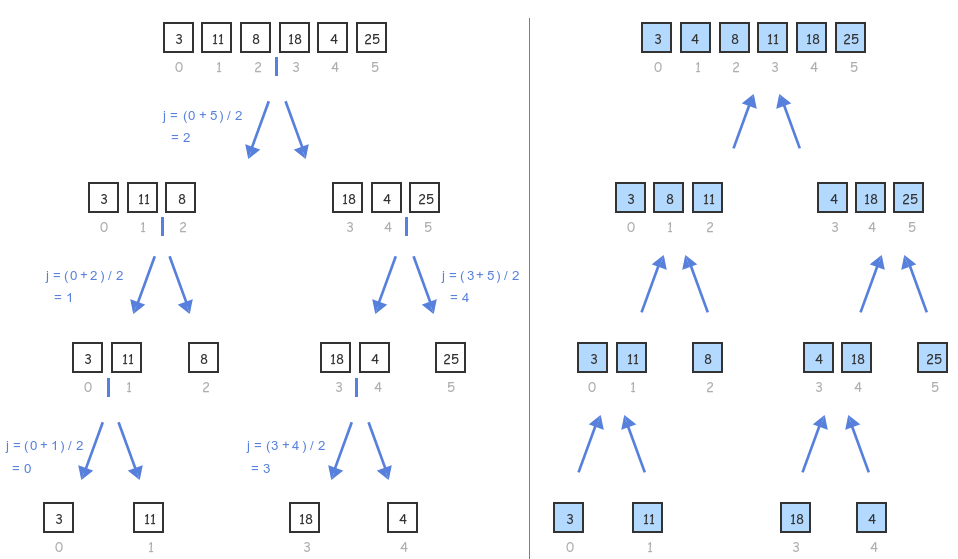
4. Merge Sort Complexity
-
The merge sort algorithm's runtime is O(N log N).
- Merge sort divides the input in half until a list of 1 element is reached, which requires log N partitioning levels. At each level, the algorithm does about N comparisons selecting and copying elements from the left and right partitions, yielding N * log N comparisons.
- Merge sort requires O(N) additional memory elements for the temporary array of merged elements.
- For the final merge operation, the temporary list has the same number of elements as the input. Some sorting algorithms sort the list elements in place and require no additional memory, but are more complex to write and understand.
- To allocate the temporary array, the Merge() function dynamically allocates the array.
- mergedNumbers is a pointer variable that points to the dynamically allocated array, and new int[mergedSize] allocates the array with mergedSize elements. Alternatively, instead of allocating the array within the Merge() function, a temporary array with the same size as the array being sorted can be passed as an argument.
5. Quick Sort
-
qsort() is available in <cstdlib>
Sorting an array of integers: tictoc/ main.cc or vecr/ tictoc.cc
int compare( const void *v1, const void *v2) // comparison function for qsort() { const int *d1 = (const int *)v1, *d2 = (const int *)v2; if( *d1 < *d2) return -1; else if( *d1 > *d2) return +1; else return 0; } void quicksort( int d[], size_t n) // qsort() interface { qsort( d, n, sizeof(int), compare); } int main() { ... quicksort( data, n); // sort data array of size n ...
6. Measuring CPU and Elapsed Time
-
tictoc/ tictoc.h or
vecr/ tictoc.cc
#include <iostream> #include <ctime> #include <chrono> using namespace std; class tictoc // tic() to start timer, toc() to stop { public: double CPU, Elapsed; tictoc() { CPU=Elapsed=0; tic(); } void print(ostream &out=cout) { out<<" CPU: "<<CPU<<endl<<" Elapsed: "<<Elapsed<<endl; } void tic() { CPU_start=clock(); Elapsed_start=chrono::high_resolution_clock::now(); } void toc() { CPU=(clock()-CPU_start)/CLOCKS_PER_SEC; chrono::duration<double> e=chrono::high_resolution_clock::now()-Elapsed_start; Elapsed=e.count(); } private: double CPU_start; chrono::system_clock::time_point Elapsed_start; };