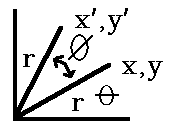
Example of a 2D rotation through an angle φ where the coordinates x, y go into x', y'. Note that φ is positive for a counterclockwise rotation and that the rotation is about the origin (0, 0).
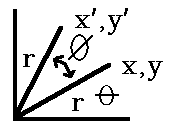
(old coordinates are (x, y) and the new coordinates are (x', y'))
θ = initial angle, φ = angle of rotation.
x = r cos θ
y = r sin θ
x' = r cos ( θ + φ ) = r cos θ cos φ - r sin θ
sin φ
y' = r sin ( θ + φ ) = r sin θ cos φ
+ r cos θ sin φ
hence:
x' = x cos φ - y sin φ
y' = y cos φ + x sin φ