---

1. Detecting Data Corruption

checksum = any small fixed-size function of a set of data

Simplest checksum: XOR (add with no carry)

data = 0x365ec4cdba148a92ecef2c3a40bef666

0011 0110 0101 1110 1100 0100 1100 1101
1011 1010 0001 0100 1000 1010 1001 0010
1110 1100 1110 1111 0010 1100 0011 1010
0100 0000 1011 1110 1111 0110 0110 0110
---- ---- ---- ---- ---- ---- ---- ----
0010 0000 0001 1011 1001 0100 0000 0011 = checksum = 0x201b9403

Can detect any single bit change.

Alternatives: add (with carry), Fletcher checksum, cyclic redundancy check (CRC), message digest (secure hash), digital signature

checksum.py:

add = 0; xor = 0; fletcher_a, fletcher_b = 0, 0

for value in values:
    add = (add + value) % 256
    xor = xor ^ value
    fletcher_a = (fletcher_a + value) % 255
    fletcher_b = (fletcher_b + fletcher_a) % 255

---

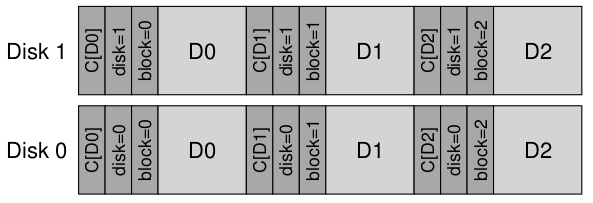
2. Checksum Disk Layout

Without checksums:

With checksums:

Block storage:

Extra checks:

Other info: inode number?

---

3. Exercises - Q1

Exercises from the book using checksum.py

Recommended change so -D option can use other bases:

$ diff checksum.py.ORIG checksum.py
48c48
<         values.append(int(t))
---
>         values.append(int(t,0)) # automatic base detection, 0b1010..., 0xabc, etc.
$

Q1:

$ python ./checksum.py Decimal: 216 194 107 66 Hex: 0xd8 0xc2 0x6b 0x42 Bin: 0b11011000 0b11000010 0b01101011 0b01000010 Add: ? Xor: ? Fletcher: ? --> check by hand $ python ./checksum.py -c Decimal: 216 194 107 66 Hex: 0xd8 0xc2 0x6b 0x42 Bin: 0b11011000 0b11000010 0b01101011 0b01000010 Add: 71 (0b01000111) Xor: 51 (0b00110011) Fletcher(a,b): 73,196 (0b01001001,0b11000100) Xor Add 11011000 11011000 11000010 11000010 01101011 01101011 01000010 01000010 -------- --------

$ python3 >>> d = [216, 194, 107, 66] >>> X = d[0]^d[1]^d[2]^d[3] >>> X 51 >>> bin(X) '0b110011' >>> A = d[0]+d[1]+d[2]+d[3] >>> A 583 >>> A % 256 71 >>> A & 0xff 71 >>> A % 255 73 >>> A0 = d[0]; A1 = A0+d[1]; A2 = A1+d[2]; A3 = A2+d[3] >>> (A0+A1+A2+A3) % 255 196 >>>

---

4. Exercises - Q3-8

3. Sometimes the additive and XOR-based checksums produce the same checksum (e.g., if the data value is all zeroes). Can you pass in a 4-byte data value (using the -D flag, e.g., -D a,b,c,d) that does not contain only zeroes and leads the additive and XOR-based checksum having the same value? In general, when does this occur? Check that you are correct with the -c flag.

4. Now pass in a 4-byte value that you know will produce a different checksum values for additive and XOR. In general, when does this occur?

5. Use the simulator to compute checksums twice (once each for a different set of numbers). The two number strings should be different (e.g., -D a1,b1,c1,d1 the first time and -D a2,b2,c2,d2 the second) but should produce the same additive checksum. In general, when will the additive checksum be the same, even though the data values are different? Check your specific answer with the -c flag.

6. Now do the same for the XOR checksum.

7. Now let's look at a specific set of data values. The first is: -D 1,2,3,4. What will the different checksums (additive, XOR, Fletcher) be for this data? Now compare it to computing these checksums over -D 4,3,2,1. What do you notice about these three checksums? How does Fletcher compare to the other two? How is Fletcher generally "better" than something like the simple additive checksum?

8. No checksum is perfect. Given a particular input of your choosing, can you find other data values that lead to the same Fletcher checksum? When, in general, does this occur? Start with a simple data string (e.g., -D 0,1,2,3) and see if you can replace one of those numbers but end up with the same Fletcher checksum. As always, use -c to check your answers.