Alice + Bob
~ q: (0.285804,0.958288) (0,0) (0,0) (0,0)
~ E: 0 0
~ H1: (0.202094,0.677612) (0,0) (-0.0171906,0.706898) (0,0)
~ E: 0 0
~ CX10: (0.202094,0.677612) (0,0) (0,0) (-0.0171906,0.706898)
~ E: 1 1
Alice
~ X1: (0,0) (-0.0171906,0.706898) (0.202094,0.677612) (0,0)
~ E: 1 1
~ Z1: (0,0) (-0.0171906,0.706898) (-0.202094,-0.677612) (0,0)
~ E: 1 1
Bob
~ CX10: (0,0) (-0.0171906,0.706898) (0,0) (-0.202094,-0.677612)
~ E: 0 0
~ H1: (0,0) (-0.296127,0.0883184) (0,0) (-0.0231213,0.950775)
~ E: 0 0
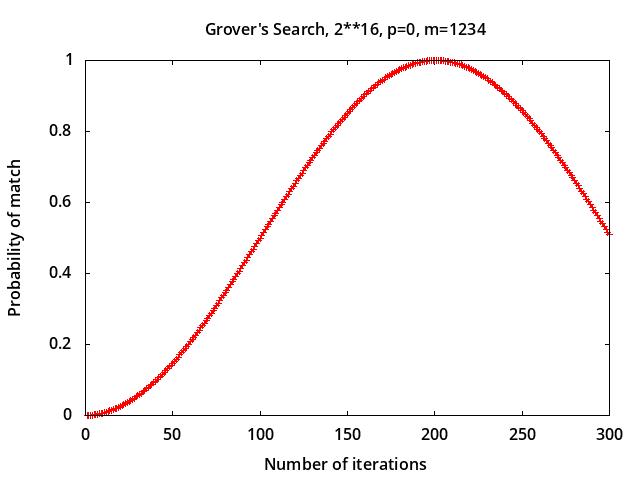
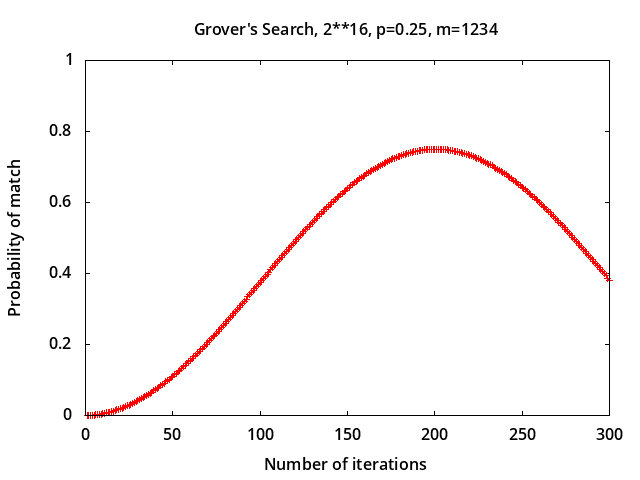
~ P(3) = 0.904508
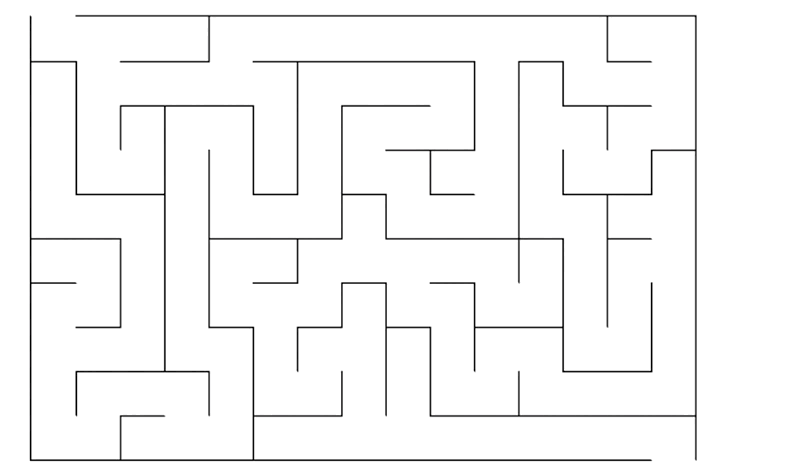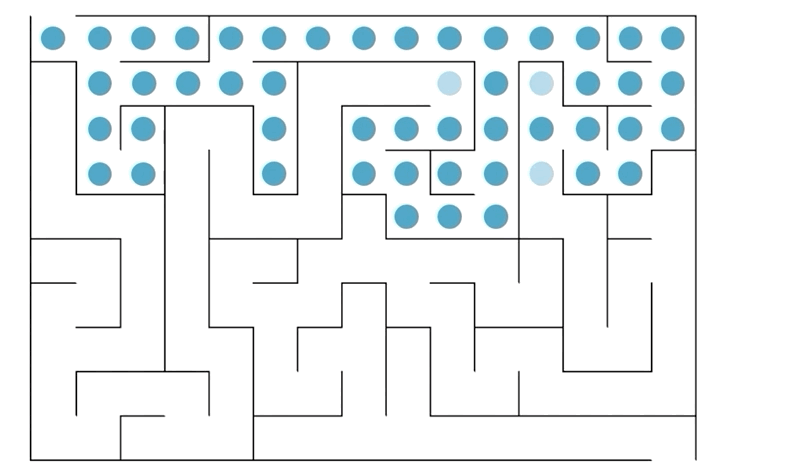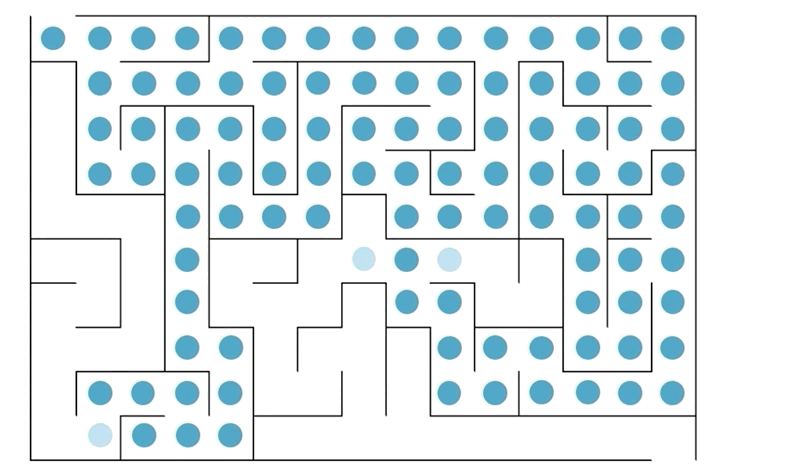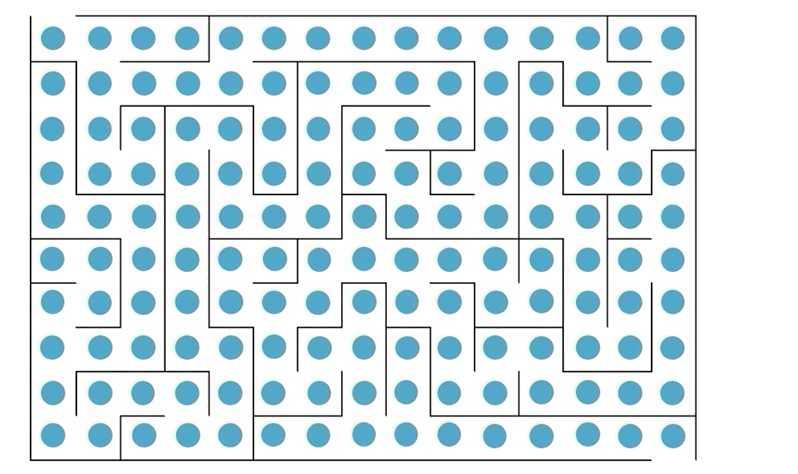

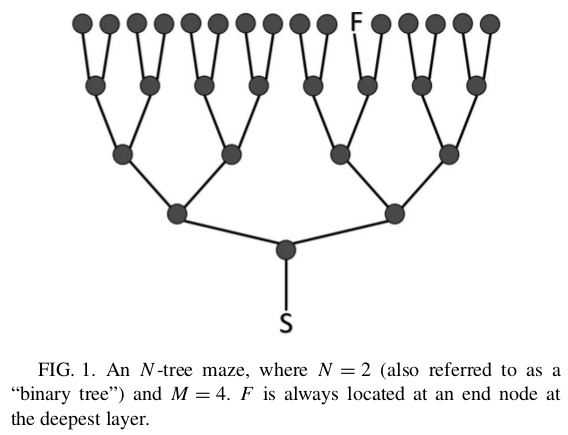
 (animations: normal, sequential)
(animations: normal, sequential)