


Next: EM and ML Sequence
Up: EM Algorithm for Sequence Channels
Previous: Introduction
Communication System Model
In the discrete-time FIR model of a time-varying noisy communications channel
with inter-symbol interference, for a block of N received data values,
the complex received data rk at time k is given by:
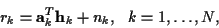 |
(1) |
where
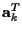 is a complex row vector containing transmitted data
{
is a complex row vector containing transmitted data
{
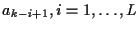 }, L is the FIR channel length,
}, L is the FIR channel length,
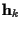 is a complex column vector containing the channel impulse response coefficients
(which are unknown) at time k, and
nk is the white Gaussian complex noise at time k with variance
is a complex column vector containing the channel impulse response coefficients
(which are unknown) at time k, and
nk is the white Gaussian complex noise at time k with variance 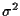 .
For
.
For 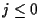 ,
the transmitted data aj may be either known (e.g. all 0's),
unknown, or estimated with some associated probabilities from the end of
a previous data block.
,
the transmitted data aj may be either known (e.g. all 0's),
unknown, or estimated with some associated probabilities from the end of
a previous data block.
Let
![${\bf H} = [{\bf h}_1, \ldots , {\bf h}_N]$](img12.gif) represent the matrix
of channel coefficient vectors over time arranged by columns,
represent the matrix
of channel coefficient vectors over time arranged by columns,
![${\bf A} = [{\bf a}_1, \ldots , {\bf a}_N]^T$](img13.gif) the
matrix of transmitted data arranged by rows, and
the
matrix of transmitted data arranged by rows, and
![${\bf r} = [ r_1 , \ldots , r_N ]^T$](img14.gif) the column vector
of received data.
With this notation, the probability density function of the received
data, given
the column vector
of received data.
With this notation, the probability density function of the received
data, given 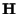 and
and 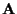 ,
is:
,
is:
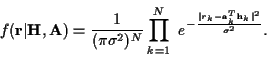 |
(2) |



Next: EM and ML Sequence
Up: EM Algorithm for Sequence Channels
Previous: Introduction
Rick Perry
2000-03-30
![]() represent the matrix
of channel coefficient vectors over time arranged by columns,
represent the matrix
of channel coefficient vectors over time arranged by columns,
![]() the
matrix of transmitted data arranged by rows, and
the
matrix of transmitted data arranged by rows, and
![]() the column vector
of received data.
With this notation, the probability density function of the received
data, given
the column vector
of received data.
With this notation, the probability density function of the received
data, given ![]() and
and ![]() ,
is:
,
is: