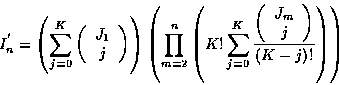Next: Bayesian Track Estimation
Up: Problem Formulation
Previous: Candidate Tracks
Now consider a set of K tracks. Assume tracks can not share detections,
and again assume missed detections are possible. It can be shown that the
number of candidate track sets is
3
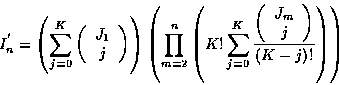 |
(6) |
Let the ith candidate K-track set be represented as
where the superscript lk (i) denotes the kth track of the ithtrack set.
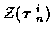 will be used to denote
the measurement data associated with the ith K-track set.
will be used to denote
the measurement data associated with the ith K-track set.
Rick Perry
1999-03-10