Following are the results of some Monte-Carlo simulations related to the report "EM ISI with time-varying channel coefficients, R. Perry, 15 May 1999".
Using 10000 trials, with one iteration of each algorithm for each trial, and L=3, with h generated as independent Gaussian random variables with mean 1 and variance 0.5, and (-1,1) data values generated with p(1)=p(-1)=0.5 for each trial, with N=16, BER results are:
EM algorithm
SNR deterministic h Gaussian h known channel
0 0.29151 0.25322 0.2441
4 0.22931 0.16076 0.15703
8 0.17908 0.067881 0.067369
12 0.15307 0.020319 0.020313
Here is a plot corresponding to the above table:

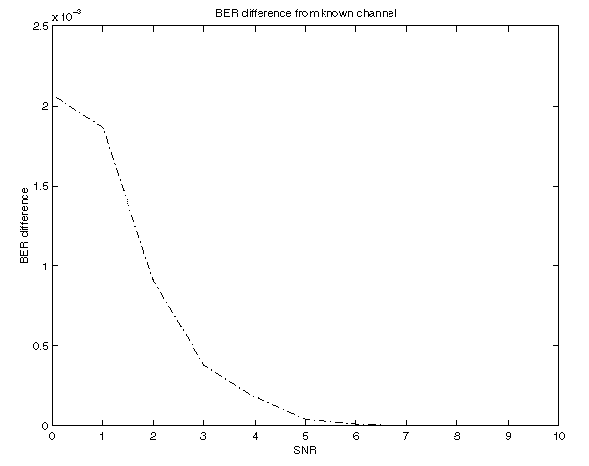
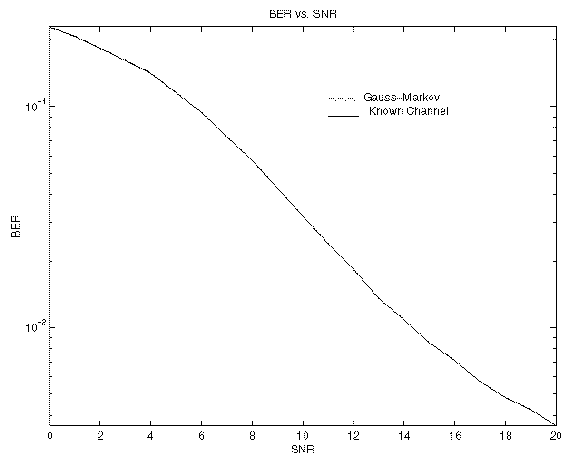
Using 10000 trials, with two iterations of EM for each trial, and L=3, with h generated using a first-order Gauss-Markov process with a=0.8 and N=16, BER results are:
SNR Gauss-Markov Known-Channel
--- ------------ -------------
0 0.23102 0.2294
1 0.20827 0.20772
2 0.18399 0.18354
3 0.16179 0.16117
4 0.14179 0.14129
5 0.11578 0.11538
6 0.094181 0.094119
7 0.073081 0.072894
8 0.057112 0.05705
9 0.042694 0.042619
10 0.031919 0.031894
11 0.023987 0.023981
12 0.01835 0.01835
13 0.013525 0.013525
14 0.010837 0.010837
15 0.0085188 0.0085188
16 0.0070812 0.0070812
17 0.0056875 0.0056875
18 0.0048125 0.0048125
19 0.0042438 0.0042438
20 0.0035875 0.0035875
Here is a plot corresponding to the above table:
The previous simulation used time-varying noise (based on the magnitude of the time-varying channel coefficients) to produce constant SNR in each set of trials. That is not the best way to do this.
For the following results, the noise variance was set constant for each SNR based on the theoretical variance of the channel coefficients. Results are similar to those above.
SNR Gauss-Markov Known-Channel
--- ------------ -------------
0 0.24019 0.23812
1 0.21957 0.2177
2 0.19754 0.19663
3 0.17677 0.17639
4 0.15474 0.15456
5 0.13257 0.13253
6 0.11351 0.1135
7 0.097519 0.097519
8 0.078231 0.078231
9 0.065363 0.065363
10 0.053394 0.053394