L-list == L-best ?

The figure below shows a scenario with two states, and the numbers on the Viterbi trellis state transition diagram indicate the total cost for each path to any point. The incremental cost of state transitions is variable, to simulate the effect of a Kalman cost function in a target tracking application. The incremental costs are not labeled on the arrows since they can be inferred from the end points.

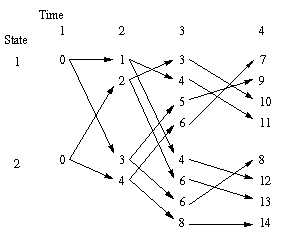
For example, a transition from state 1 at time 1 to state 2 at time 2 has an incremental cost of 3. A transition from the Kalman filter at state 1 at time 2 with cost 1 to state 1 at time 3 has an incremental cost of 3.

For time 1, 2, and 3, all possible state transitions are shown. For time 4, only the lowest cost 4 transitions to each state are shown out of the 8 possible transitions.

From this figure, we can easily backtrack through the trellis to find the lowest cost path. At time 4, the lowest cost possibility has a cost of 7, with predecessor state 3, and the corresponding lowest cost path through the states is:

2 -> 2 -> 1 -> 1

The 2nd best path has a cost of 8 with the state sequence:

1 -> 2 -> 2 -> 2

But suppose that, at each time instant, we only saved the lowest cost transitions to each state, which is what the standard Viterbi algorithm does. At time 2, we'd only save the path to state 1 having cost 1. That path leads to a cost of 4 at time 3, which leads to a cost of 11 at time 4. The other lowest cost transitions for state 2 end up with a final total cost of 12. Thus the final result would be a path having cost 11 and the state sequence:

1 -> 1 -> 1 -> 1

That state sequence does not have minimal cost, which was shown above to be 7. The conclusion is, using a variable cost function such as a Kalman filter, one must keep track of more than just the best path to each state, such as by using the List Viterbi algorithm [1], in order to find the overall best path. Also, if one wants to produce the L-best paths, one must keep track of more than L possible paths at each time instant.

[1]
	N. Seshadri and C. Sundberg, "List Viterbi Decoding Algorithms with Applications", IEEE Trans. on Communications, Vol. 42, No. 2/3/4, Feb./March/April 1994, pp. 313-323.