Quantum Computing & Cryptography

Outline

1. Background

2. Physics

3. Math

4. Simulation

5. Breaking Cryptography

6. Post-Quantum Cryptography

      Eniac 1950:   30 tons, 150 KW, 1 KB, 100 KHz

      Phone 2020:   5 oz., 1 W, 4 GB, 2 GHz

      QC 2020:   tons, KW, 50 qubits, 1 MHz

      QC 2050:   ???

Ion Trap Quantum Device

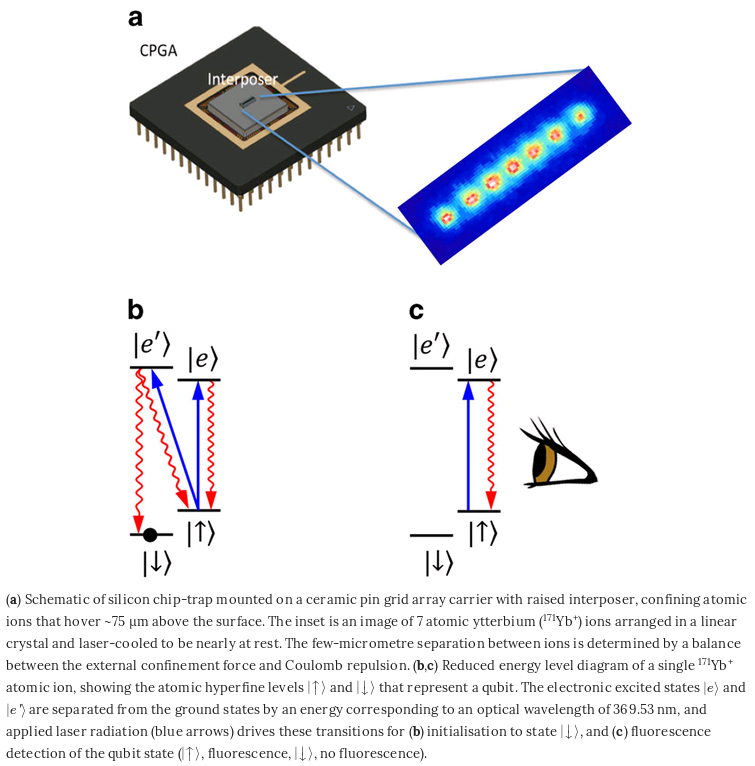
Co-designing a scalable quantum computer with trapped atomic ions, Kenneth R Brown, Jungsang Kim & Christopher Monroe, Nature 2016.
---

Quantum Key Distribution

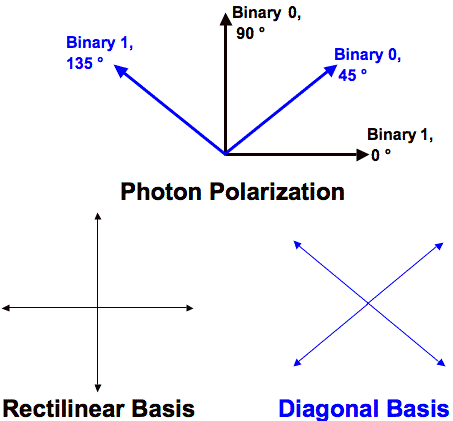
A Survey of the Prominent Quantum Key Distribution Protocols, Mart Haitjema. Figure 2, corrected.
---

Quantum Key Distribution

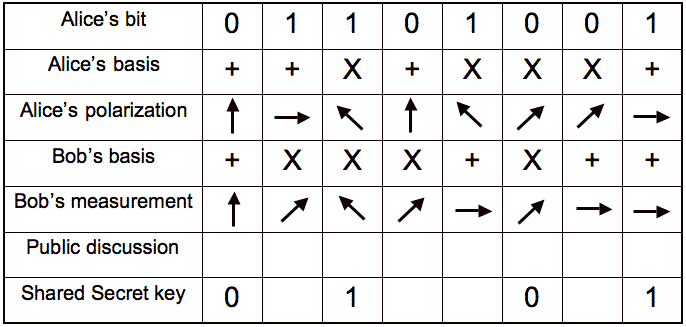
Alice's bits:	secret
Alice's basis:	initially secret, public later
Alice's polarization:	secret
Bob's basis:	public
Bob's measurement:	secret

      Schrödinger Equation

Complex state vector Ψ:   |Ψ_i|² = Prob(measure state i)

Hamiltonian matrix H, Hermitian:   H^† = H

Unitary matrix U:   U^-1 = U^†

      One Qubit

Superposition:   α |0> + β |1>

Complex Amplitudes:   α,   β

Probabilities:   |α|²,   |β|²

An Introduction to Quantum Computing, Without the Physics, Giacomo Nannicini, 2017 (2020).
---

      Single Qubit Operations

Superposition

An Introduction to Quantum Computing, Without the Physics, Giacomo Nannicini, 2017 (2020).
---

      Two Qubits

Entanglement

An Introduction to Quantum Computing, Without the Physics, Giacomo Nannicini, 2017 (2020).
---

CNOT:   creating entangled states

~   initially a = |0>+|1>, b = |0>

~   q   a b   p -> a b⊕a              class TwoQubit:
~   0   0 0  0.5   0 0  0.5             def cnot(self):
~   1   0 1        0 1                      '''Controlled NOT operation'''
~   2   1 0  0.5   1 0                      self.onezero, self.oneone = self.oneone, self.onezero
~   3   1 1        1 1  0.5                 return self

~   Using an array:                     Using names for the complex amplitudes:

~   q[0], q[1], q[2], q[3]              zerozero, zeroone, onezero, oneone

~   swap q[2] and q[3]                  Python Quantum Computing simulator, Juliana Peña, 2011.

Simulation:   n qubits -> 2ⁿ complex state amplitudes

1 q0 q1

2 q0 q1 q2 q3

3 q0 q1 q2 q3 q4 q5 q6 q7

4 q0 q1 q2 q3 q4 q5 q6 q7 q8 q9 q10 q11 q12 q13 q14 q15

5 q0 q1 q2 q3 q4 q5 q6 q7 q8 q9 q10 q11 q12 q13 q14 q15 q16 q17 q18 q19 q20 q21 q22 q23 q24 q25 q26 q27 q28 q29 q30 q31

Simulation:   distributed computing

For n=33 qubits, 128 GB of memory is required just for the array of quantum amplitudes. On a single 128 GB node this causes swapping, and the run-time increases to 43832 seconds (about 12 hours) which is a factor of 36 times what would be expected following the exponential scaling (20 minutes). For n=34 qubits a single node has insufficient memory and can not perform the simulation.

Grover's Search (1996):   Quadratic Speedup

• Search space of size 2ⁿ using 2^(n/2) function evaluations vs. classical (2ⁿ)/2

• Security implications: 256-bit key for ANY algorithm will have only 128-bit security level

• Simulation:

  ~   for( iter = 1; iter <= k; ++iter)
  ~   {
  ~    // apply f, i.e. flip sign of state m
  ~    //
  ~     q[m] = -q[m];
  
  ~    // inversion about the average
  ~    //
  ~     avg = 0;  for( i = 0; i < N; ++i) avg += q[i];
  
  ~     avg *= 2.0/N;  for( i = 0; i < N; ++i) q[i] = avg - q[i];
  ~   }    
  

Grover's Search:   inversion about the average

An Introduction to Quantum Computing, Without the Physics, Giacomo Nannicini, 2017 (2020).
---

Grover's Search:   16-bit Example

• 2¹⁶ = 65536 possibilities, would take (2¹⁶)/2 = 32768 iterations on average classically
  • Takes only (π/4)2^(16/2) = 201 quantum iterations optimally, success probability 0.999988

Shor factoring (1994):   breaking RSA

• Quantum evaluation of ya mod N for random y, and ALL a at once

• Determine period r, mod N: y^r = 1, so (y^r/2 - 1)*(y^r/2 + 1) = 0 -> will share factor with N

Shor factoring example:   N = 33

• DFT probability peaks (205, 410, 614, 819, ...) produce period estimates (9.9902, 4.9951, 3.3355, 2.5006, ...)

• Using r = 10 ≈ 9.9902: (5^10/2 - 1)*(5^10/2 + 1) = 22*24
  • gcd(22,N) = 11,   gcd(24,N) = 3,   both factors of N

Post-Quantum Cryptography

• NIST = National Institute of Standards and Technology

• Standardizing one or more quantum-resistant public-key cryptographic algorithms

• For use on classical computers

• Must be resistant to classical and quantum computing attacks

• Second-round candidate algorithms include:
  • 17 public-key encryption and key-establishment algorithms

  • 9 algorithms for digital signatures

• "A wide range of mathematical ideas are represented by these algorithms... to hedge against the possibility that if someone breaks one, we could still use another."

• pqcrypto.org - Dan Bernstein's post-quantum cryptography resources

NIST Post-Quantum-Cryptography-Standardization

NIST Reveals 26 Algorithms Advancing to the Post-Quantum Crypto 'Semifinals'

References

1. An Introduction to Quantum Computing, Without the Physics, Giacomo Nannicini, 2017 (2020). arxiv.org/abs/1708.03684

2. Python Quantum Computing simulator, Juliana Pena, 2011. Two qubits and superdense coding protocol example. gist.github.com/limitedmage/945473

3. Quantum Computing Emulation, R. Perry, 2018-2020. fog.misty.com/perry/qce/notes.html

---

Hackers of the Future

Already planning attacks on quantum computers:

4. An entangling-probe attack on Shor's algorithm for factorization, Hiroo Azuma, 2017. arxiv.org/abs/1705.00271 : an attacker can steal an exact solution of Shor's algorithm outside an institute where the quantum computer is installed if he replaces its initialized quantum register with entangled qubits.