 |
 |
The source code AMP.cc is part of the QCE quantum computing emulator.
In Quantum Wordle Visualization an optimization was shown for problems where there is at least one state which does not correspond to any solution. By initializing the state amplitudes to specific values, the optimum number of Grover iterations can be forced to be an integer, leading to a solution with probability 1. But setting arbitrary state amplitudes is inefficient and can require exponentially many gates [2,3]. Simpler alternative methods to optimize the search are described in [4], using an extra qubit or a fractional final rotation, which will be demonstrated here.
For the unstructured quantum search problem,
let |w> represent the desired solution state,
|s> the initial state,
and |s'> the projection of |s> onto
the orthogonal complement of |w> [1].
Let θ/2 represent the angle between
|s> and |s'>.
Then a=sin(θ/2) is the amplitude of the projection of
|s> onto |w>, i.e. the amount of
|s> which is in the |w> direction.
Starting with the current state |q> initialized to |s>,
each iteration of the Grover algorithm rotates |q> by an angle
θ towards |w>.
After r iterations the angle between
|q> and |s'> will be (r+1/2)θ.
So the number of iterations required to make
that angle π/2,
so |q> is equal to |w>,
is r=(π/2)/θ-1/2.
In general r is not an integer, so it must be rounded up to an
integer number of iterations k=⌈r⌉, which results
in a solution measurement probability less than 1.
Using n qubits with N=2n states
initialized to a uniform superposition using Hadamard transformations:
a=1/sqrt(N),
|s>=H|0...0|, and the initial state amplitude vector
is a*[1,...,1].
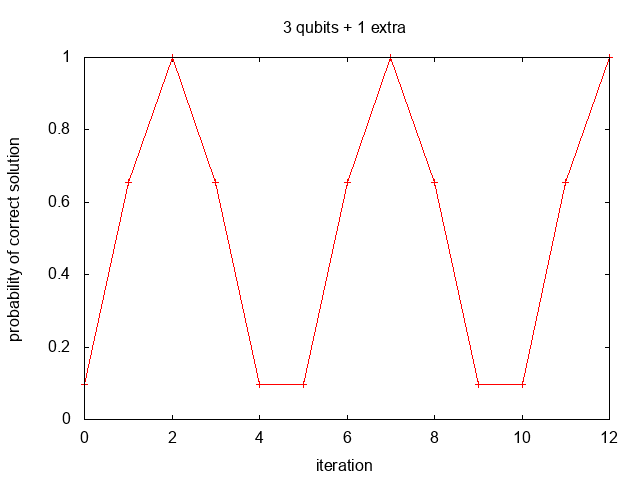
By using an extra qubit the rotation angle and initial state can be chosen so that
after an integer number of iterations the solution measurement probability will be exactly 1:
let θk=(π/2)/(k+1/2),
A=sin(θk/2),
B=sqrt(a2-A2), and
|s>=X|0>H|0...0|,
where X=[A B; B -A]/a and
the initial state amplitude vector of length 2N is
A*[1,...,1],B*[1,...,1].
The Grover rotation operator 2|s><s|-I
does not correspond to inversion about the mean in this case,
since the amplitudes of the initial state are not uniform.
In a simulation the rotation can be implemented directly by maintaining
a copy of |s>, or more efficiently by just using
A and B.
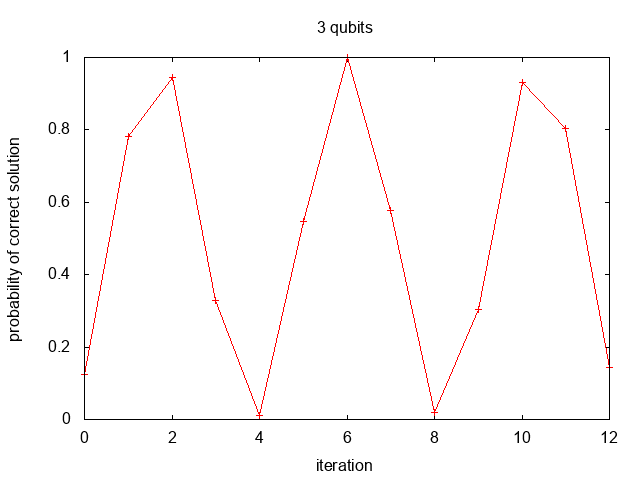
For an example, with N=8 using 3 qubits the optimum number of
iterations is r=1.67341. Using 2 iterations produces the suboptimal
solution measurement probability 0.945312
but using an extra qubit with rotation angle and initial state chosen as described above
produces the solution with probability 1 after 2 iterations:
 |
 |
Corresponding simulation text output displays the probability, one minus the probability, and index number of the correct solution and the two most likely measurements for each iteration: 3 qubits, 3 qubits + 1 extra.
Instead of rounding up the optimal number of iterations r to an integer,
consider rounding down to k=⌊r⌋, then using k
standard Grover rotations, followed by a fractional final rotation:
G(φ0,φ1) = -H S0 H S1
where S1 multiplies the amplitude of the desired solution state
by eiφ1,
and S0 multiplies the amplitude of the zero state
by eiφ0 [4].
G(π,π) is the standard Grover rotation, where the multiplicative
factors are both -1. But φ0 and
φ1 can be chosen to achieve a desired fractional rotation
as will be shown further below.
The operation -H S0 H generalizes the method of
inversion about the mean originally presented by Grover [5]:
-H S0 H = H (R - I) H, with R = diag(1-eiφ0, 0, ...,0)
= H R H - H I H
= H R H - I, since H = H-1
This may also be written in terms of the initial state uniform superposition |s>=H|0>:
-H S0 H = (1-eiφ0)|s><s| - I
The elements of the matrix multiplication H R H are:
[H R H]j,m = ∑k,l Hj,k Rk,l Hl,m
= ∑k,l (-1)j·k/√N Rk,l (-1)l·m/√N
= (-1)j·0 (1-eiφ0) (-1)0·m / N, since Rk,l=0 except for k=l=0
= (1-eiφ0)/N
Thus all elements of the matrix H R H
are equal to (1-eiφ0)/N.
The operation q'=(H R H - I)q on the components of state vector q
is equivalent to:
qk' = (1-eiφ0)∑qj/N - qk
which is the same as inversion about the mean if φ0=π.
The orthonormal coordinate system |w>,|s'> will be used
to determine the angles φ0 and φ1
using the constants c=sqrt(N), d=sqrt(N-1) and relations:
|s> = (1/c)|w> + (d/c)|s'>
|s'> = (c/d)|s> - (1/d)|w>
|w> = c|s> - d|s'>
Considering the operations S1 and -H S0 H separately:
S1 |w> = eiφ1 |w>, S1 |s'> = |s'>
-H S0 H |w> = [(1-eiφ0)|s><s| - I] |w>
= (1-eiφ0)|s><s|[c|s> - d|s'>] - |w>
= (1-eiφ0)|s>[c - dd/c] - |w>
= (1-eiφ0)|s>/c - |w>
= (1-eiφ0)[(1/c)|w> + (d/c)|s'>]/c - |w>
= [(1-eiφ0-N)/N]|w> + [(1-eiφ0)d/N]|s'>
-H S0 H |s'> = -H S0 H [(c/d)|s> - (1/d)|w>]
= [(1-eiφ0)|s><s|-I](c/d)|s> + H S0 H (1/d)|w>
= -eiφ0(c/d)|s> + (1/d) H S0 H |w>
= -eiφ0(c/d)[(1/c)|w> + (d/c)|s'>] - (1/d)[((1-eiφ0-N)/N)|w> + ((1-eiφ0)d/N)|s'>]
= (1/d)[-eiφ0-(1-eiφ0-N)/N]|w> + [-eiφ0-(1-eiφ0)/N]|s'>
= [(1-eiφ0)d/N]|w> + [(-eiφ0(N-1)-1)/N]|s'>
Combining the S1 and -H S0 H operations,
the overall rotation is:
G(φ0,φ1)|w> = [eiφ1(1-eiφ0-N)/N]|w> + [eiφ1(1-eiφ0)d/N]|s'>
G(φ0,φ1)|s'> = [(1-eiφ0)d/N]|w> + [(-eiφ0(N-1)-1)/N]|s'>
After k standard Grover rotations
the state is x|w>+y|s'>,
with x=sin((k+1/2)θ) and y=cos((k+1/2)θ),
where θ=2sin-1(1/sqrt(N)) [1].
The fractional final rotation must produce state |q>=|w>,
i.e. the |s'> component of
G(φ0,φ1)(x|w>+y|s'>)
must be zero:
[eiφ1(1-eiφ0)d/N]x + [(-eiφ0(N-1)-1)/N]y = 0
In general this constraint can be solved classically
for φ0 and φ1
using a numerical method such as Nelder-Mead simplex [6].
For n=1 qubits (N=2) the exact analytical solution is
φ0=φ1=π/2.
In this case a standard Grover rotation produces the suboptimal solution
measurement probability 0.5, whereas a fractional rotation produces
the correct solution with probability 1. Of course in this degenerate case
after a single guess one will know either that the guess is correct, or that
the guess is wrong and the alternative guess is correct, since there are only
2 possibilities.
For n=2 qubits (N=4) the exact analytical solution is
φ0=φ1=π, so the
standard and fractional rotations are the same and both produce
the correct solution with probability 1 after one rotation.
For standard Grover rotations the probability of incorrect measurement decreases as the number of qubits increases, due to the smaller angular discrepancy between the integer number of rotations and the optimal non-integer number. Using a fractional final rotation, the theoretical probability of incorrect measurement is zero, but due to finite precision the computed probability grows as roundoff errors accumulate:
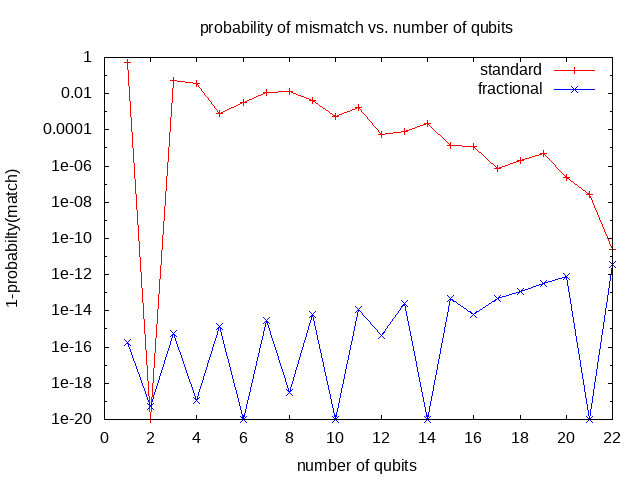
Standard vs. Fractional Final Rotation
long double was used in computing the above simulation
results, and any probabilities that were computed as 0
(or slightly negative due to roundoff errors)
were set to 1e-20. At 22 qubits the inaccuracy of the standard Grover rotations,
due to angular discrepancy, and the inaccuracy of the fractional final rotation,
due to accumulated roundoff errors, are about the same.
[1] Grover's algorithm, Wikipedia, https://en.wikipedia.org/wiki/Grover's_algorithm
[2] Option Pricing using Quantum Computers, Nikitas Stamatopoulos, Daniel J. Egger, Yue Sun, Christa Zoufal, Raban Iten, Ning Shen, and Stefan Woerner, July 2020, https://arxiv.org/abs/1905.02666
[3] Quantum-state preparation with universal gate decompositions, Martin Plesch and Caslav Brukner, March 2011, https://arxiv.org/abs/1003.5760
[4] Quantum Amplitude Amplification and Estimation, Gilles Brassard, Peter Hoyer, Michele Mosca, and Alain Tapp, May 2000, https://arxiv.org/abs/quant-ph/0005055
[5] Quantum Mechanics Helps in Searching for a Needle in a Haystack, Lov K. Grover, Physical Review Letters, Vol. 79, No. 2, July 1997, pp. 325-328, https://arxiv.org/abs/quant-ph/9706033
[6] Nelder-Mead Simplex Optimization, Wikipedia, https://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method