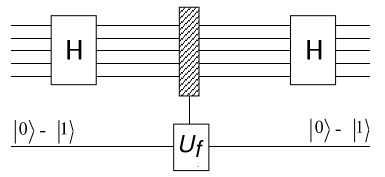
Figure 1. Network representation of Deutsch-Jozsa algorithm ([2] Figure 4)
Abstract
The Deutsch-Jozsa quantum algorithm can determine if a hidden Boolean function
is constant or balanced with just one function evaluation on a superposition of
the N possible input values, whereas a classical solution must
evaluate the function up to 1+N/2 times [1,2].
For N=2 the problem is analogous to determining whether a coin
is fair or biased [3,4]. Here we detail and extend the coin analogy
for N≥2 and derive results for general coins
which are not necessarily constant or balanced.
Introduction
A coin is hidden in a box, and also in the box is a tiny genie named Fred who can answer questions about the coin. For example, you can ask Fred about one side of the coin and he will reply 1 if that side is heads, or 0 if that side is tails.
You communicate with Fred by invoking
a function F(X), where X represents the
side number of the coin and the sides are numbered starting with 0.
So for a 2-sided coin you can call F(0) and F(1) and if Fred replies
1 for one and 0 for the other then you know the coin is fair.
Otherwise the coin is biased, with both sides heads or both sides tails.
In general for an N-sided coin you can call F(X)
with X=0,1,...,N-1 and Fred will reply with 1 if that side
is heads, or 0 if that side is tails or does not exist (X≥N).
A 6-sided coin, for example, is like
a dice but instead of the sides being labeled with the numbers 1 to 6 they
are each labeled H or T. For an N-sided coin to be fair,
N must be even, with N/2 sides labeled H
and N/2 sides labeled T.
A 2-sided coin is either fair or fake.
Randomly selecting one side, i.e. flipping it, if the probability of heads
is p, then the probability of tails is 1-p,
with p=1/2 for a fair coin, but p=0 or
p=1 for a fake coin. We assume that the coin is
equally likely to land on either side when flipping it.
An N-sided coin
can have varying degrees of bias when N is greater than 2.
For example, a 6-sided coin with 4 sides labeled H is biased with p=4/6.
But with 5 sides labeled H it is even more biased with p=5/6.
Deutsch-Jozsa Algorithm
If Fred was a classical genie, he could only answer questions for one X value
at a time, so determining p for an N-sided coin
would require N calls to F(X). But our Fred is
a quantum genie, so he can answer questions with a superposition of X values.
By asking Fred just one question, with a superposition of all possible X values,
the Deutsch-Jozsa algorithm can determine whether F(X) is constant or balanced,
assuming F(X) is restricted to being constant or balanced.
If the number of sides on the coin is a power of 2, then for a fair coin
F(X) will be balanced.
For the more general case we will have to take a different approach.
Note that simply evaluating F(X) with a superposition of all possible X values
does not directly provide a useful result. Although F(X) will contain a superposition of
results, you can not see these in a physical quantum system
(though you can see them in a simulation),
and when measured you will only obtain one of the possible values.
The Deutsch-Jozsa algorithm provides a useful result by applying a Hadamard transformation to
F(X) and then measuring; this single measurement can then distinguish between
constant and balanced functions, although it can not determine exactly which constant or balanced
function is present (e.g. whether a constant function corresponds to the coin being always heads
or always tails).
This is similar to other famous quantum algorithms which apply a transformation before
measuring, such as inversion about the mean for Grover's search algorithm, and the Fourier transform
for Shor's factoring algorithm.
Consider the Deutsch-Jozsa algorithm [2]
when the number of sides on the coin is a power of 2 (N=2n):

Figure 1. Network representation of Deutsch-Jozsa algorithm ([2] Figure 4)
The lines entering on the top-left represent n
input qubits which are each initialized to |0> and then transformed by Hadamard H
into a superposition of all possible X values 0,1,...,N-1.
Fred's function F(X) is implemented by the Uf gate
which performs the operation:
Uf|X>|Y> = |X>|Y⊕F(X)>
Uf is an auxiliary qubit
Y=|0>-|1>, which can be produced by performing a Hadamard transformation on |1>,
and the output from Uf is:
|X> (|0⊕F(X)> - |1⊕F(X)>) = (-1)F(X) |X> (|0> - |1>)
F(X)=0 and F(X)=1.
Uf leaves Y unchanged but
flips the sign on X values for which F(X)=1
(see notes on Interference and Quantum Computations
regarding quantum gates affecting their input qubits).
If F(X) is constant, then the output from the second Hadamard H is:
(±1)H|X> = (±1)|0>,
i.e. the second Hadamard undoes the first one, so measuring those qubits
will always yield |0>.
If F(X) is balanced, then the amplitude of output state |0>
will be 0, since the signs of the |0> terms in the superposition output
will be (-1)F(X), i.e. half of them 1 and half -1, which will cancel
in summation, so that state will never be observed(1).
So if F(X) is restricted to being constant or balanced, then measuring
state |0> means it is constant and measuring anything else
means it is balanced.
The following table shows the probabilities for measuring state values at the output of
the Deutsch-Jozsa algorithm for n=3 and various distributions of heads and tails
on the coin. The bit positions of R are 1 for heads and 0 for tails corresponding
to the possible X values, so for example R=11111111 means all heads and
R=10010000 means heads only for X=0 and X=3.
X\R | 00000000 | 11111111 | 00101011 | 01110100 | 10010000 | 10010100 |
|---|---|---|---|---|---|---|
| 000 | 1 | 1 | 0 | 0 | 0.25 | 0.0625 |
| 001 | 0 | 0 | 0.25 | 0.25 | 0 | 0.0625 |
| 010 | 0 | 0 | 0.25 | 0 | 0 | 0.0625 |
| 011 | 0 | 0 | 0 | 0.25 | 0.25 | 0.0625 |
| 100 | 0 | 0 | 0.25 | 0.25 | 0.25 | 0.0625 |
| 101 | 0 | 0 | 0 | 0 | 0 | 0.0625 |
| 110 | 0 | 0 | 0 | 0.25 | 0 | 0.0625 |
| 111 | 0 | 0 | 0.25 | 0 | 0.25 | 0.5625 |
Table 1. State Measurement Probabilities: X = state, R = position of heads
Only the first four columns, which have a 1 or 0 probability in the first row for X=000,
represent meaningful results for the Deutsch-Jozsa algorithm.
These columns show results for all tails (F(X) constant), all heads (constant),
and two different distributions of 4 heads (balanced) respectively.
The last two columns correspond to non-constant non-balanced F(X),
with 2 heads and 3 heads respectively.
However, the last column also represents the case of a fair (balanced) 6-sided coin with 3 heads,
which the Deutsch-Jozsa algorithm can not handle properly since the number of sides
is not a power of 2.
Consider running the Deutsch-Jozsa algorithm multiple times for each of the cases in the table.
For the first two cases (F(X) constant) the measured state will always be
X=000, and for the second two cases (balanced) the measured state may vary
but will never be X=000. For these four cases there is no point in running the
algorithm multiple times, once is sufficient and if state X=000 is measured
we conclude that F(X) is constant, otherwise it is balanced.
For the fifth case, with 2 heads, the measured state is equally likely to be
X=000, X=011, X=100, or X=111.
Simulation experiments indicate that in general with N sides and 2 heads
half of the state values are possible to be measured.
To detect this case the Deutsch-Jozsa algorithm
would have to be run at least N/2 times, and would be no more efficient
than the classical algorithm which just evaluates F(X) separately
for each X.
For the sixth case, with 3 heads, any of the possible states may be measured,
with X=111 the most likely.
Simulation experiments indicate that in general with N sides and 3 heads
all of the state values are possible to be measured, with some states more likely depending on
the positions of the heads.
Similar to the fifth case,
running the Deutsch-Jozsa algorithm multiple times to detect this case would
not be efficient.
Coin Search Algorithm
To determine the probability of heads for an N-sided coin,
with N not necessarily a power of 2, our genie Fred
and the Deutsch-Jozsa algorithm are not very helpful.
But fortunately Fred has a brother, George, who is also in the box
and can answer questions about the coin. For example, you can ask George
if the coin has exactly 3 heads and he will reply 1 if that is true or 0 if that is false.
You communicate with George by invoking a function G(X), where X
represents the number of heads you are asking about.
For a 2-sided coin you can call G(1) and if George replies 1 then you know the coin is fair.
Similarly for an N-sided coin you can call G(N/2) and if George replies 1
then you know the coin is fair.
If G(N/2) is 0 then we know the coin is not fair, but since we do not know the number of heads
we do not know how unfair it is. To determine the number of heads
we could evaluate G(X) for X = 0, 1, ..., N and stop when we receive a 1.
This would take N/2 calls to G(X) on average for a uniform distribution of coins.
However, like Fred, George is also a quantum genie,
so he can answer questions with a superposition of X values.
Consider what happens if we ask George a question
with a superposition of all possible X values and then
transform that result to make it more useful.
Similar to Figure 1, but using quantum gate Ug to implement George's
G(X) function,
and then performing a transformation W instead of H,
the output is:
W Ug|X> = W (-1)G(X) |X>
G(X) is only 1 when X equals the correct number of heads,
and is 0 for all other X values, the (-1)G(X) factor
simply flips the sign of one X value. Then the transformation W
is designed to increase the probability of measuring that particular value.
This is Grover's algorithm [5]. W is an inversion about the mean
which replaces each state amplitude a with (2ã-a)
where ã is the average amplitude. Application of
Ug and W can be repeated
to increase the desired probability further, up to a point.
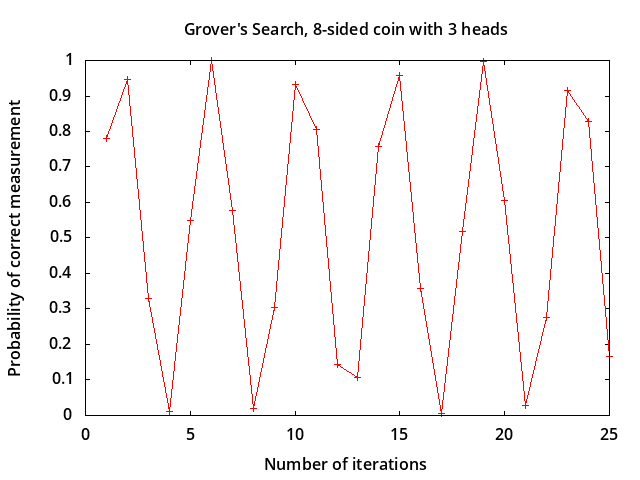
The following table shows the probabilities for measuring state values after each iteration of Grover's algorithm for a coin with 3 heads.
X\iter | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0.125 | 0.03125 | 0.0078125 | 0.0957031 |
| 1 | 0.125 | 0.03125 | 0.0078125 | 0.0957031 |
| 2 | 0.125 | 0.03125 | 0.0078125 | 0.0957031 |
| 3 | 0.125 | 0.78125 | 0.945312 | 0.330078 |
| 4 | 0.125 | 0.03125 | 0.0078125 | 0.0957031 |
| 5 | 0.125 | 0.03125 | 0.0078125 | 0.0957031 |
| 6 | 0.125 | 0.03125 | 0.0078125 | 0.0957031 |
| 7 | 0.125 | 0.03125 | 0.0078125 | 0.0957031 |
Table 2. State Measurement Probabilities vs. Iteration Number - 3 heads
Initially the probabilities are all equal to 0.125 before applying
Ug and W.
After one iteration the probability of measuring X=3
is increased to 0.78125.
After the second iteration the probability is increased further to 0.945312
but after the third iteration it decreases.
For Grover's algorithm in general it can be shown that the probability of measuring
the correct value is maximized by performing k≈sqrt(N)π/4 iterations
[5],
i.e. k≈2.2214 for N=8.
A 256-sided coin would require only k≈12.566 iterations compared with
N/2=128 guesses on average for a classical search.
The probability is periodic in the number of iterations, as shown in Figure 2:
 |
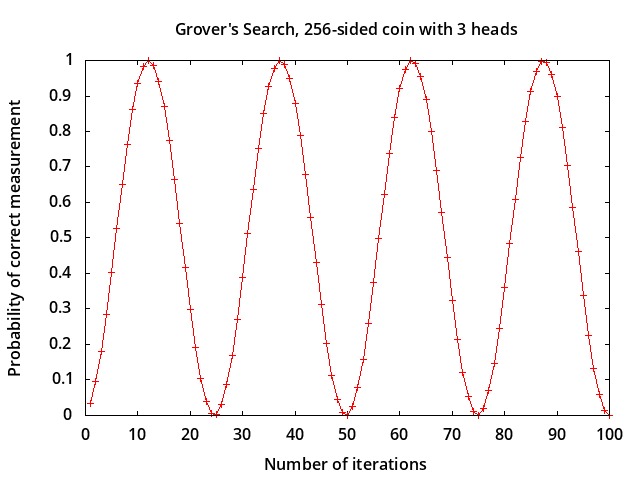 |
Figure 2. Grover's Search, Probability of correct measurement
[1] The Deutsch-Jozsa Problem: De-quantisation and Entanglement, Alastair A. Abbott, 2010.
[2] Quantum algorithms revisited, R. Cleve, A. Ekert, C. Macchiavello, M. Mosca, Proc. R. Soc. Lond. A (1998) 454, 339-354. This is reference #6 from [1].
[3] Quantum Computation and Quantum Communication: Theory and Experiments, Mladen Pavicic, Springer, 2006.

[4] Experimental realization of a quantum algorithm, Isaac L. Chuang, Lieven M.K. Vandersypen, Xinlan Zhou, Debbie W. Leung, and Seth Lloyd, 1998.
To determine whether such a function is constant or balanced is analogous to determining whether a coin is fair - with heads on one side and tails on the other; or fake - with heads on both sides. Classically, one must look at the coin twice, first one side then the other, to determine if it is fair or fake. The D-J algorithm exploits quantum coherence to determine if a quantum 'coin' is fair or fake while looking at it only once.
(1)
For example, in matrix/vector form with n=2, the second Hadamard operation is
(omitting normalization factors):
H (-1)F(X) |X> = |
|
|
= |
|