1. Introduction
SS is a batch spreadsheet processor for C programmers. It produces a spreadsheet display from plain text input files, similar to the way documents are created using LaTeX. The resulting display is not interactive. A shell script front-end is also provided for preprocessing (using the C preprocessor) and post-processing to generate HTML or graphics output.SS includes all of the numeric operators from the C programming language, with the same syntax, precedence, and associativity as C. It also includes all of the functions from the C90 (ANSI/ISO 9899:1990) standard library math.h, all of the non-complex functions from the C99 standard library tgmath.h, as well as other numeric and range functions. It allows cycles and non-convergent iterative formulas.
2. Input and Output
SS reads input from files specified on the command line, or from standard input if no file names are specified. The pseudo input file name "-" can also be used to explicitly specify reading standard input. All of the input is filtered through the C preprocessor. All formulas and commands must be terminated with a semicolon.Output goes to standard output by default, but can be redirected globally using the output command, or redirected on a per-command basis using the plot and print commands. "stdout" and "-", with or without quotes, can be used as pseudo output file names to refer to standard output.
The spreadsheet row/column output begins with a line starting with a tab followed by the column headings separated by tabs. Then, for each row, the output begins a new line starting with the row number followed by a tab followed by the cell values (or formulas or pointers) separated by tabs.
For plotting, the output consists of one or two (plot2d) or three (plot3d) columns of numbers, preceded by a line starting with a tab.
3. Command-line Options
The spreadsheet is normally run using the SS shell script which invokes the C preprocessor (to handle #include and #define directives, and remove comments) and has options related to post-processing for generating HTML and plot output. The ss compiled executable itself has options for debugging and setting the size of the spreadsheet array. The executable can be run directly if pre- and post-processing are not needed.Both SS and ss support the -h, --help command-line option which displays a usage summary to standard error:
Usage: SS [-H|--HTML|--html] [-t|--title title] [-T|--Table|--table] [-p|-p2|--plot|--plot2d|-p3|--plot3D] [-x|--xlabel xlabel] [-y|--ylabel ylabel] [-z|--zlabel zlabel] [ss options...] [file...] Usage: ss [-h|--help] [-d|--debug] [-v|--verbose] [--version] [-r|--rows #rows] [-c|--cols #cols]The -T option produces HTML table output without any <html>, <head>, or <body> tags, suitable for embedding in an HTML document.
The -t option sets the title for HTML or plot output.
The -x, -y, -z options set the x, y, z axis labels for plot output. Gnuplot is used to produce plots.
The default number of rows (1000) and columns (702) in the spreadsheet may be overridden using the -r and -c options. The -v or --verbose option displays the row and column index ranges:
% SS -v < /dev/null ss: rows 0...999, cols 0...701 (A...ZZ) % SS -c 10000 --verbose < /dev/null ss: rows 0...999, cols 0...9999 (A...NTP) %
4. Cells - A0 Format
In A0 format, cells are specified by their column (one or more letters, case-insensitive) and row (one or more digits), with an optional '$' preceding the column and/or row value to indicate that the cell is fixed.The column value represents an integer column number as follows for the default spreadsheet size:
column: letters A B C ... Z AA AB AC ... AZ BA BB BC ... BZ ... ZZ integer 0 1 2 ... 25 26 27 28 ... 51 52 53 54 ... 77 ... 701Example cell specifications:
a2 - relative $a2 - fixed column, relative row aa$31 - fixed row, relative column $b$100 - fixed row, fixed columnWhen copying formulas, relative cell references remain relative to the destination cells, and fixed references remain fixed.
Example:
b1 = 10*a1 + $d$0;
copy b2:b5 b1:b4;
print b1:b5 formulas;
B
1 (10*A1)+$D$0
2 (10*A2)+$D$0
3 (10*A3)+$D$0
4 (10*A4)+$D$0
5 (10*A5)+$D$0
5. Cells - RC/CR Formats
In RC and CR formats, cells are specified by their row and column numbers, using the letters R and C (or r, c), with brackets around relative offsets.For example, relative to cell D2:
r0C0 - fixed row 0, fixed column 0 (same as C0R0 or A0) R1c2 - fixed row 1, fixed column 2 (same as C2R1 or C1) C[-2]R[] - relative column -2, same row, i.e. B2, relative to D2 R[-2]C[0] - relative row -2, same column, i.e. D0, relative to D2 R[1]C[+1] - relative row +1, relative column +1, i.e. E3, relative to D2 R[]C[] - relative row and column, no offsets, i.e. D2 relative to D2The format command can be used to change the format for printing formulas from A0 (the default) to RC or CR.
Example:
b1 = 10*a1 + $d$0;
copy b2:b5 b1:b4;
format RC; print b1:b5 formulas;
1
1 (10*R[]C[-1])+R0C3
2 (10*R[]C[-1])+R0C3
3 (10*R[]C[-1])+R0C3
4 (10*R[]C[-1])+R0C3
5 (10*R[]C[-1])+R0C3
6. Ranges
A range consists of two cells, the start and end cells of the range, separated by a colon.
For example, A0:B9 (or A0:C1R9, or R0C0:R9C1, or C0R0:R9C1, etc.)
specifies a range including rows 0 to 9 of columns A and B.
The range start and end values do not have to be
in increasing order; B9:A0, B0:A9, and A9:B0 all refer to the same group of
cells as A0:B9, but correspond to different directions for traversing the
range. For example the command copy a0:a9 b9:b0 would copy column b to a
in reverse order.
By default, ranges are traversed byrows to improve cache performance, since elements in a row are adjacent in memory. That is, in pseudo-code:
for row = start_row to end_row
for col = start_col to end_col
use cell[row,col]
The bycols option can be used globally or with
various commands (copy, eval, fill, etc.)
to cause evaluation by columns.
That is, in pseudo-code:
for col = start_col to end_col
for row = start_row to end_row
use cell[row,col]
Note that the starting row may be less than, equal to, or greater than the
ending row. Same for columns. So a range may consist of a single cell,
row, or column (a0:a0, a0:d0, a0:a4), cells in "increasing" order (a0:b4), or
cells in "partial decreasing" order (a4:b0, b0:a4), or cells in "decreasing"
order (b4:a0).
A range basically represents a list of cells, and is explicitly converted to a list when used as a numeric function argument.
A range consisting of a single cell may be specified using just that one cell, e.g. A0 as a range is the same as A0:A0.
7. Primitive Data Types
The SS primitive data types are:
- double precision floating point
- All numeric calculations are performed and stored using
double precision floating point.
The cast operators, (int) and (long), can be used to truncate an expression to integral form, and the resulting integer will be stored using double precision floating point.
- string
- A string is a sequence of characters enclosed in 'single' or "double" quotes.
No escape sequences are recognized. Adjacent strings are concatenated into
one string.
If a string occurs in
a numeric calculation it is treated as having the value 0.0
- constant
- The built-in constants are:
HUGE_VAL = inf DBL_EPSILON = 2.22045e-16 RAND_MAX = 2.14748e+09
The values of the constants may vary depending on the system. To check the values of the constants use commands help or print constants.
8. Symbols
User-defined variables are stored in a symbol table.Cell references in symbol formulas are fixed since there is no destination cell reference. Relative cell references in symbol formulas (e.g. r[1]c[2]) are relative to cell A0, and so are equivalent to fixed references (e.g. r1c2).
Note that cell names can not be used as symbols.
Example:
% cat syms.ss pi = 4*atan(1); d2r = d*pi/180; d = 90; a = 29; a0 = pi; ca = a0; b0 = ca; 2*3*4*5; eval; print all; % ss < syms.ss
pi = 4*atan(1) = 3.14159 d2r = (d*pi)/180 = 1.5708 d = 90 a = 29 ca = A0 = 3.14159 $1 = ((2*3)*4)*5 = 120 A B 0 pi ca A B 0 3.14 3.14For unnamed expressions such as 2*3*4*5 above, names $1, $2, etc. are automatically generated. These auto-names are for reference only and can not be used explicitly in any formulas or expressions.
9. Operators
SS includes all of the numeric operators from C, with the same precedence, associativity, and meaning.SS also includes operators ** for exponentiation, ^^ for logical XOR, and the logical assignment operators &&=, ^^=, and ||=. The keywords NOT, AND, XOR, and OR, case-insensitive, may also be used to represent the logical operators.
SS does not include the C array, structure, and pointer operators.
The operators are:
() parentheses, (expr) ++ postfix increment, x++ -- postfix decrement, x-- ++ prefix increment, ++x -- prefix decrement, --x - unary minus + unary plus ~ bitwise NOT ! logical NOT NOT logical NOT (int) cast (long) cast (double) cast ** exponentiation, x**y == pow(x,y) * multiplication / division % mod, x%y == fmod(x,y) + addition - subtraction << shift left, x<<y == x*2**y >> shift right, x>>y == x/2**y < less than <= less than or equal > greater than >= greater than or equal == equal != not equal & bitwise AND ^ bitwise XOR | bitwise OR && logical AND AND logical AND ^^ logical XOR XOR logical XOR || logical OR OR logical OR ?: conditional operator, e1 ? e2 : e3 = assignment *= multiplication assignment /= division assignment %= mod assignment += addition assignment -= subtraction assignment <<= shift left assignment >>= shift right assignment &= bitwise AND assignment ^= bitwise XOR assignment |= bitwise OR assignment &&= logical AND assignment ^^= logical XOR assignment ||= logical OR assignment , comma operatorThe bit shift operators <<, <<=, >>, and >>= are implemented for floating-point using ldexp() to adjust the binary exponent by the specified power of 2. For the other bitwise operators, the floating-point operands are converted to long integers to perform the operations.
10. Numeric Functions
The numeric functions include all of the functions from the C90 standard library math.h, all of the non-complex functions from C99 tgmath.h (i.e. all except carg, cimag, conj, cproj, and creal), as well as rand from stdlib.h, time from time.h, and the scaled pseudo-random number generators drand, irand, and nrand.Most of the numeric functions take one expression argument and return one value. A few of the functions take no arguments (drand, nrand, rand, time, row, col), and some take two or three arguments. frexp, modf, and remquo can return two values.
The numeric functions are:
acos arc cosine
acosh inverse hyperbolic cosine
asin arc sine
asinh inverse hyperbolic sine
atan two-quadrant arctangent
atan2 four-quadrant arctangent, atan2(y,x) ~= atan(y/x)
atanh inverse hyperbolic tangent
cbrt cube root
ceil ceiling
col cell column number
copysign copy sign of a number
cos cosine
cosh hyperbolic cosine
drand pseudo-random double, 0.0 <= drand() < 1.0
erf error function
erfc complementary error function
exp exponential
exp2 base-2 exponential
expm1 exponential minus 1, expm1(x) == exp(x) - 1
fabs absolute value
fdim positive difference
floor floor
fma floating-point multiply and add
fmax maximum of two values
fmin minimum of two values
fmod mod, x%y == fmod(x,y)
frexp extract fraction and exponent, {f,e} = frexp(x)
hypot Euclidean distance
ilogb extract exponent
irand pseudo-random integer, 0 <= irand(i) <= i-1
ldexp ldexp(x,e) produces x * (2**e)
lgamma log gamma function
llrint round to nearest integer
llround round to nearest integer
log natural logarithm
log10 base 10 logarithm
log1p logarithm of 1 plus argument, log1p(x) == log(1+x)
log2 base 2 logarithm
logb extract exponent
lrint round to nearest integer
lround round to nearest integer
modf extract fraction and integral parts, {f,i} = modf(x)
nearbyint round to nearest integer
nextafter nextafter(x,y) == next value following x in the direction of y
nexttoward nexttoward(x,y) == next value following x in the direction of y
nrand pseudo-random normal (Gaussian) -6.0 <= nrand() < 6.0
pow exponentiation, x**y == pow(x,y)
rand pseudo-random integer, 0 <= rand() <= RAND_MAX
remainder remainder(x,y) == remainder of dividing x by y
remquo remainder and part of quotient, {r,q} = remquo(x,y)
rint round to nearest integer
round round to nearest integer
row cell row number
scalbln scalbln(x,e) produces x * (FLT_RADIX**e)
scalbn scalbn(x,e) produces x * (FLT_RADIX**e)
sin sine
sinh hyperbolic sine
sqrt square root
tan tangent
tanh hyperbolic tangent
tgamma gamma function
time time in seconds since 00:00:00 UTC, January 1, 1970
trunc round to integer, towards zero
Notes:
The pseudo-random number generator functions are initialized using
srand(time()) when the program is run, but you can
reinitialize using the srand command.
nrand is a simple approximate truncated Gaussian distribution computed as the sum of 12 uniform samples minus 6.
11. Range Functions
Range functions take an argument list of expressions and ranges and return one or more values.The range functions are:
avg average of the defined cells
count number of cells defined
dot dot product (inner product) of two ranges
feval val=feval("type",cr,x), evaluate parameterized function
llsq {rank,cr}=llsq("type",xr,yr), linear least squares
majority non-zero if majority of defined cells are non-zero
max maximum of the defined cells
min minimum of the defined cells
prod product of the defined cells
search {xr}=search(f,x0[,dx[,x1...xN]]), search for minimum of f(xr)
stats {a,s,l,h}=stats(...), avg, stdev, min, and max of the defined cells
stdev standard deviation of the defined cells
sum sum of the defined cells
var variance of the defined cells
Additional information:
dot dot product (inner product) of two ranges
- The dot product dot(x,y) is the sum of the pairwise products of the elements
of the x and y ranges, which must have the same size:
dot(x,y) = x0 y0 + x1 y1 + x2 y2 + ...
feval val=feval("type",cr,x), evaluate parameterized function- The function is evaluated at the point x using parameters specified
by the range cr.
Available function types are:
- "poly"
- A polynomial in the following form:
c0 + c1 x + c2 x2 + c3 x3 + ...
The polynomial is evaluated using Horner's rule. For example, using 4 coefficients:c0 + x*(c1 + x*(c2 + x*c3))
- (When other function types are implemented they will be documented here)
llsq {rank,cr}=llsq("type",xr,yr), linear least squares- Solves for the least square error approximation for y as a function of
x.
If type is "data", then no basis functions are used, and y is approximated as a direct linear combination of the data with coefficients specified by the range cr:
y = c0 x0 + c1 x1 + c2 x2 + ...
The xr input data range size must equal the product of the sizes of cr and yr.If type is not "data", then y is approximated using a linear combination of basis functions
f0, f1, f2, ...:y = c0 f0(x) + c1 f1(x) + c2 f2(x) + ...
In this case, the xr and yr input data ranges must be the same size.The result coefficients are stored in cr, so the size of that range determines the number of data points or basis functions to be used in the approximation for each y value.
The return value is the rank of the matrix which is constructed to solve for the coefficients, as determined by a singular value decomposition.
Available basis function types are:
- "poly"
- The polynomial basis functions are:
1, x, x2, x3, ... - (When other basis function types are implemented they will be documented here)
search {xr}=search(f,x0[,dx[,x1...xN]]), search for minimum of f(xr)- Determines values for the N
elements of range xr which minimize the function
defined by the cell or symbol formula f.
Uses the Nelder-Mead simplex algorithm for unconstrained non-linear
function minimization.
x0 specifies the initial value for xr. Optionally, dx specifies step sizes used to create the initial simplex, and x1...xN specifies the initial simplex vertices. If x1...xN are specified then dx is only used for restarts. If dx is not specified then a default step size of +10% in each direction is used. x0, dx, and x1...xN may be expression lists or ranges.
The following variables can be used to modify the tolerances and limits used by search:
symbol name default value description ----------- ------------- ----------- search_func_limit 200*N limit on number of function evaluations search_func_tol 10-4 function tolerance search_size_tol 10-4 simplex size tolerance search_cond_check 5*N how often to check condition number search_cond_limit 104 limit on condition number for restart
The search terminates successfully when the difference between the highest and lowest function values is less than or equal to search_func_tol and the simplex size (a measure of the deviation in the xr values) is less than or equal to search_size_tol. The search terminates unsuccessfully and displays a warning if the number of function evaluations reaches search_func_limit.In some cases the search algorithm can get stuck and converge to a non-minimum point. This behavior can be detected by monitoring the condition number of the matrix of simplex directions, checking it every search_cond_check iterations. If the condition number exceeds search_cond_limit then the search is restarted using orthogonal steps around the current lowest point.
- Search Tips:
- To maximize a function, define the formula to be the
negative of the desired function.
To find a zero of a function, define the formula to be the absolute value of the desired function.
If the formula is defined in a symbol and search produces warnings about cyclic dependencies, try defining the formula in a cell instead.
For debugging, set debug on to cause search to produce detailed output as it proceeds.
12. Multiple Assignments
A range may be assigned using a list of expressions with the following syntax:
range = { e1, e2, ... }
If the list contains fewer elements than the range being assigned,
the list will be traversed more than once. If the list contains
too many elements a warning message will be displayed.
The list can contain empty elements to skip the associated cell assignments:
% cat expr_list.ss a0:c2 = { 1, , 3, 4,, 6}; print values; % ss < expr_list.ss
A B C 0 1.00 3.00 1 4.00 6.00 2 1.00 3.00
Some functions can return more than one value. The syntax for assigning multiple return values uses braces for grouping:
{ r1, r2, ... } = func(...)
where r1, r2, etc. may be symbols, cells, or ranges.
For example:
{ f, e} = frexp( a); // get fraction and exponent
{ a0, s, c0:d0} = stats( g0:g9); // get avg, stdev, min, and max
{ c0:d0} = stats( g0:g9); // just get avg and stdev
{a0} = stats( g0:g9); // just get avg, formula is in cell a0
a0 = stats( g0:g9); // same as above
Formulas which use multiple return values
are stored in the symbol table, and are evaluated whenever the symbol
table is evaluated.
They are automatically named $1, $2, etc.
13. Commands
Unlike formulas, which are stored and evaluated later, commands are not stored and are executed immediately.Numeric expressions in command arguments are evaluated in dependency order.
SS commands are:
byrows|bycols - set default direction
copy [byrows|bycols] dest_range src_range
debug [on|off|level]
eval [byrows|bycols] [range|symbols] [number_of_iterations]
exit
fill [byrows|bycols] range
fill [byrows|bycols] range start_expr, increment_expr
fill [byrows|bycols] range { expr_list }
fill [byrows|bycols] range "fmt", "start", increments...
format A0|RC|CR - formula printing format
format [cell|row|col|range|symbols] "fmt_string"
headers on|off
help - print list of operators, functions, commands and constants
help ["what"] - print help matching string
output "fname" - redirect output to a file
plot|plot2d|plot3d ["fname"] [byrows|bycols] [range]
print ["fname"] [byrows|bycols] [range] [all|constants|...
...|formats|formulas|functions|pointers|states|symbols|values]...
quit
reset [range|symbols] - set formulas to unevaluated state
srand expr - initialize the pseudo-random number generator
Additional information:
- copy [byrows|bycols] dest_range src_range
- If the source range contains fewer elements than the destination
it will be traversed more than once. If the source range contains
too many elements a warning message will be displayed.
A more general way of assigning a range is using a multiple assignment
as discussed in the previous section,
for example
A1:A9 = { A0 }; - eval [byrows|bycols] [range|symbols]
-
If the number of iterations is not specified,
then the cells and/or symbols are evaluated
in dependency order. This will fail and display an error
message if any cyclic dependencies are encountered.
If no range or symbols options are specified, then all of the cells and symbols are evaluated. If range or symbols options are specified, then only that range and/or the symbols are evaluated, in dependency order, which can cause evaluations to occur outside of the specified range if there are dependencies outside of that range.
The cells and/or symbols which are evaluated in dependency order are set to the evaluated state. This means that their formulas will not be reevaluated by subsequent dependency evaluations unless they are first reset to the unevaluated state using the reset command.
- eval [byrows|bycols] [range|symbols] number_of_iterations
-
If the number of iterations is specified, then the cells and/or symbols will be evaluated up to that number or iterations or until convergence. The state of formulas (evaluated or unevaluated) is ignored and not changed by this type of evaluation.
If no range or symbols options are specified, then each iteration will first evaluate the symbol table, then evaluate the cells twice: first starting at the top-left corner of the cells being used and traversing the range to the bottom-right corner of the cells being used; then again starting at the bottom-right corner and traversing to the top-left corner.
If only the symbols option is specified, then only the symbol table is evaluated.
If only a range is specified, then only that range is evaluated, in the default or specified direction (byrows or bycols), for the specified number of iterations.
If the symbols option and a range are both specified, then the symbol table and range are both evaluated, in the specified order, for the specified number of iterations. For example,
eval a0:a1 symbols 2;is equivalent toeval a0:a1 1; eval symbols 1; eval a0:a1 1; eval symbols 1; - fill [byrows|bycols] range
- Fill a range with constant 0,1 values suitable as inputs for a truth-table.
For example, fill a0:c7; produces 8 rows and 3 columns representing
the 8 possible 3-bit values:
A B C 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 - fill [byrows|bycols] range start_expr, increment_expr
- Fill a range with constant values, starting with the start expression value,
and increasing by the increment expression value for subsequent cells.
The start and increment expressions are evaluated only once,
before filling starts.
- fill [byrows|bycols] range { expr_list }
- Fill a range using a list of expressions. Unlike the range assignment
statement, the fill command always uses each of the expressions in the list
exactly once, so the extent of the range filled is determined by the
length of the expression list rather than by the size of the specified
range. The end cell of the range determines only the direction for
traversing the range.
- fill [byrows|bycols] range "fmt", "start", increments...
- Fill a range with date/time strings, using strftime()
with the specified format. The start value can be in the form "YYYY-MM-DD"
or "HH:MM:SS" or "YYYY-MM-DD:HH:MM:SS". Defaults for omitted start date or time
values are "2000-01-01" and "12:00:00".
Depending on the form of the start value, the increments are specified in years, months, days, or hours, minutes, seconds, or both:
"YYYY-MM-DD", year_inc[,month_inc[,day_inc]] "HH:MM:SS", hour_inc[,min_inc[,sec_inc]] "YYYY-MM-DD:HH:MM:SS", year_inc[,month_inc[,day_inc[hour_inc[,min_inc[,sec_inc]]]]]
The increment expressions are evaluated only once, before filling starts.Examples (date_time.ss, date_time.out):
// fill column with: fill a0:a9 "%Y", "2012-01-01", 1; // years fill b0:b15 "%Y-%m", "2011-11-01", 0, 1; // months "YYYY-MM" fill c0:c9 "%m/%d", "2011-12-29", 0, 0, 1; // days "MM/DD" fill d0:d12 "%H:%M", "11:15:00", 0, 15; // time "HH:MM" - headers on|off
- Display of row and column headers can be controlled by the
headers command.
- format A0|RC|CR - formula printing format
- The format A0, RC, and CR options
specify the format used for printing formulas.
- format [cell|row|col|range|symbols] "fmt_string"
- For printing spreadsheet values, the format can be set globally or
for a specific cell, row, column or range.
The default global format is "%.2f".
If a cell is not assigned a format, and evaluation is byrows (the default), printing will use the cell's row format, if set; otherwise it will use the cell's column format, if set; otherwise it will use the global format.
If a cell is not assigned a format, and evaluation is bycols, printing will use the cell's column format, if set; otherwise it will use the cell's row format, if set; otherwise it will use the global format.
The default format for printing symbol table values is "%g". This can be changed using the format symbols command.
- plot|plot2d|plot3d ["fname"] [byrows|bycols] [range]
- The plot commands do not actually plot anything, they simply
display output in a form suitable for plotting to be used in conjunction
with the plot command-line options.
- print ...
- print all; is equivalent to print symbols, formulas, values;
When printing formulas, indirect dependencies on symbol table formulas (due to use of multiple return values) are shown in parentheses, e.g. ($1), ($2), etc.
14. Simple Statistical Example
Student test scores are scaled to produce grades which have an average of 80 and standard deviation of 15:% cat grades.ss a0:d0 = { "grade", "score", "avg", "stdev"}; mean = avg(b1:b5); c1 = mean; d1 = stdev(b1:b5); a1 = 80+15*(b1-mean)/$d$1; // scaled scores copy a2:a5 a1:a4; b1:b5 = { 57, 67, 92, 87, 76 }; // raw scores eval; print symbols values formulas pointers; % SS --Table grades.ss
mean = avg(B1:B5) = 75.8
| A | B | C | D | |
|---|---|---|---|---|
| 0 | grade | score | avg | stdev |
| 1 | 60.29 | 57.00 | 75.80 | 14.31 |
| 2 | 70.77 | 67.00 | ||
| 3 | 96.98 | 92.00 | ||
| 4 | 91.74 | 87.00 | ||
| 5 | 80.21 | 76.00 | ||
| A | B | C | D | |
| 0 | "grade" | "score" | "avg" | "stdev" |
| 1 | 80+((15*(B1-mean))/$D$1) | 57 | mean | stdev(B1:B5) |
| 2 | 80+((15*(B2-mean))/$D$1) | 67 | ||
| 3 | 80+((15*(B3-mean))/$D$1) | 92 | ||
| 4 | 80+((15*(B4-mean))/$D$1) | 87 | ||
| 5 | 80+((15*(B5-mean))/$D$1) | 76 | ||
| A | B | C | D | |
| 0 | 0x8ed9b88 | 0x8ed9bd8 | 0x8ed9c18 | 0x8ed9c58 |
| 1 | 0x8eda010 | (nil) | 0x8ed9d90 | 0x8ed9e30 |
| 2 | 0x8eda010 | (nil) | ||
| 3 | 0x8eda010 | (nil) | ||
| 4 | 0x8eda010 | (nil) | ||
| 5 | 0x8eda010 | (nil) |
15. Bank Balance Example
Checking account and Visa credit card transactions are combined into one spreadsheet:% cat bank.ss g2:j14 = {g1+(!c2&&d2)*(f2-e2), h1+!(c2&&d2)*(f2-e2), i1+(c2&&!d2)*e2, h2+i2}; format c "%g"; format d "%g"; g1:j1 = { 1438.62, g1, 0.00, h1+i1 }; a0:j0 = {"2012","Desc","V","x","-","+","Bank","Real","Visa","TrueBal" }; fill a2:f3 { "12/26", "Kelly's", 1, 1, 19.97, , "12/25", "Sfly", 1, 1, 25.00, , "12/25", "Netflix", 1, 1, 8.47, , "01/03", "Verizon", , 1, 100.98, , "01/04", "Mtg", , 1, 436.58, , "01/06", "AMC", 1, , 58.63, , "01/06", "Amazon", 1, , 152.64, , "01/11", "BMSS #2841", , , 10, , "01/27", "PECO", , , 223.02, , "01/22", "BSB", , 1, , 300, "01/23", "ATT", , , 195.92, , }; eval; headers off; print; % SS -c 10 --Table bank.ssVisa charges are marked with a 1 in column C. Transactions which have been processed by the bank and Visa charges which have been paid are marked by a 1 in column D. The balances in columns G to J use the values from columns C and D in logical expressions such as !C2&&D2 meaning the item was not a credit card transaction and was processed by the bank.
The result shows the bank balance, real balance (including credit card charges and other transactions which have not yet been processed, i.e. how much money you really have left), Visa balance, and true balance (what the bank balance would be if all transactions were processed, not including credit card charges):
| 2012 | Desc | V | x | - | + | Bank | Real | Visa | TrueBal |
| 1438.62 | 1438.62 | 0.00 | 1438.62 | ||||||
| 12/26 | Kelly's | 1 | 1 | 19.97 | 1438.62 | 1438.62 | 0.00 | 1438.62 | |
| 12/25 | Sfly | 1 | 1 | 25.00 | 1438.62 | 1438.62 | 0.00 | 1438.62 | |
| 12/25 | Netflix | 1 | 1 | 8.47 | 1438.62 | 1438.62 | 0.00 | 1438.62 | |
| 01/03 | Verizon | 1 | 100.98 | 1337.64 | 1337.64 | 0.00 | 1337.64 | ||
| 01/04 | Mtg | 1 | 436.58 | 901.06 | 901.06 | 0.00 | 901.06 | ||
| 01/06 | AMC | 1 | 58.63 | 901.06 | 842.43 | 58.63 | 901.06 | ||
| 01/06 | Amazon | 1 | 152.64 | 901.06 | 689.79 | 211.27 | 901.06 | ||
| 01/11 | BMSS #2841 | 10.00 | 901.06 | 679.79 | 211.27 | 891.06 | |||
| 01/27 | PECO | 223.02 | 901.06 | 456.77 | 211.27 | 668.04 | |||
| 01/22 | BSB | 1 | 300.00 | 1201.06 | 756.77 | 211.27 | 968.04 | ||
| 01/23 | ATT | 195.92 | 1201.06 | 560.85 | 211.27 | 772.12 | |||
| 1201.06 | 560.85 | 211.27 | 772.12 | ||||||
| 1201.06 | 560.85 | 211.27 | 772.12 |
16. Plot Example
% cat plot.ss alpha = 0.05; beta = .4; fill a0:a99 0, 0.5; b0:b99 = { exp(-alpha*a0)*cos(beta*a0) }; eval; plot a0:b99; % SS -p plot.ss > plot.gif
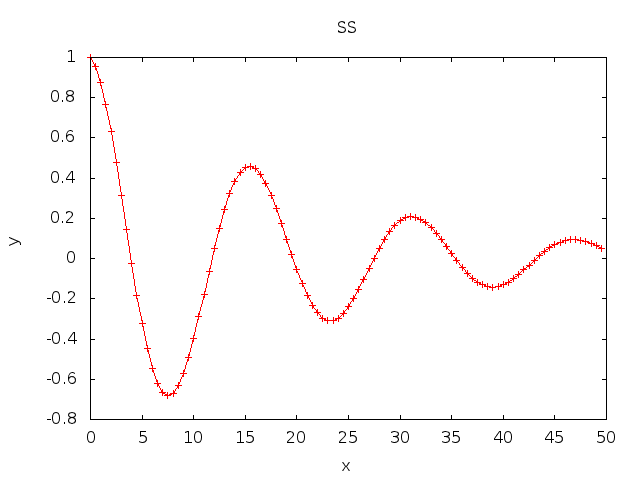
17. 3D Plot Example
% cat plot3d.ss #define N 50 #define a 0.4 #define xCell(r,c) R ## r ## C ## c #define Cell(r,c) xCell(r,c) M = ((N/2.0)-0.5); Cell(1,1):Cell(N,N) = { (sin(a*(row()-M))/(row()-M)) * (sin(a*(col()-M))/(col()-M)) }; eval; plot3d Cell(1,1):Cell(N,N); % SS -p3 plot3d.ss > plot3d.gif
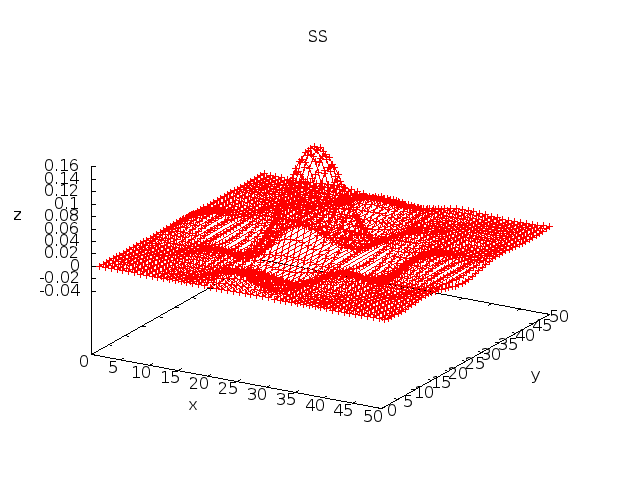
18. llsq "data" Example
% cat antelopes.ss
// From http://college.cengage.com/mathematics/brase/understandable_statistics/7e/students/datasets/mlr/frames/frame.html
// Thunder Basin Antelope Study
// The data (X1, X2, X3, X4) are for each year.
// X1 = spring fawn count/100
// X2 = size of adult antelope population/100
// X3 = annual precipitation (inches)
// X4 = winter severity index (1=mild,5=severe)
//
b0:c0 = { "Err", "Est" }; h0 = "Coeff";
fill d0:g1 {
"X1", "X2", "X3", "X4",
2.9, 9.2, 13.2, 2, // 8 sets of measured data
2.4, 8.7, 11.5, 3,
2, 7.2, 10.8, 4,
2.3, 8.5, 12.3, 2,
3.2, 9.6, 12.6, 3,
1.9, 6.8, 10.6, 5,
3.4, 9.7, 14.1, 1,
2.1, 7.9, 11.2, 3,
, , , ,
, 10, 10, 1, // predict fawn count for these inputs
, 10, 10, 3,
, 10, 10, 5
};
{rank,h1:h3} = llsq("data",e1:g8,d1:d8);
b1:c8 = { c1-d1, dot($h$1:$h$3,e1:g1) };
h5 = sqrt(dot(b1:b8,b1:b8)); // norm(Err)
c10:c12 = { dot($h$1:$h$3,e10:g10) }; // predictions
eval; format h "%.6g"; print symbols values;
% SS -T antelopes.ss
rank = 3
$1 = {rank,H1:H3} = llsq("data",E1:G8,D1:D8) = 3
| B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|
| 0 | Err | Est | X1 | X2 | X3 | X4 | Coeff |
| 1 | -0.02 | 2.88 | 2.90 | 9.20 | 13.20 | 2.00 | 0.32251 |
| 2 | 0.19 | 2.59 | 2.40 | 8.70 | 11.50 | 3.00 | 0.0103248 |
| 3 | -0.01 | 1.99 | 2.00 | 7.20 | 10.80 | 4.00 | -0.110479 |
| 4 | 0.35 | 2.65 | 2.30 | 8.50 | 12.30 | 2.00 | |
| 5 | -0.31 | 2.89 | 3.20 | 9.60 | 12.60 | 3.00 | 0.619503 |
| 6 | -0.15 | 1.75 | 1.90 | 6.80 | 10.60 | 5.00 | |
| 7 | -0.24 | 3.16 | 3.40 | 9.70 | 14.10 | 1.00 | |
| 8 | 0.23 | 2.33 | 2.10 | 7.90 | 11.20 | 3.00 | |
| 9 | |||||||
| 10 | 3.22 | 10.00 | 10.00 | 1.00 | |||
| 11 | 3.00 | 10.00 | 10.00 | 3.00 | |||
| 12 | 2.78 | 10.00 | 10.00 | 5.00 |
19. llsq "poly" Example
% cat poly.ss // creates noisy polynomial data values, // then finds LLSQ approximation to the data srand 23456; // just to make the docs reproducable, // remove to use default srand(time()) #define M 11 // number of data points #define N 3 // number of llsq coefficients #define xCell(c,r) c ## r #define Cell(c,r) xCell(c,r) #define Range(c1,r1,c2,r2) xCell(c1,r1):xCell(c2,r2) #define X Range(a,1,a,M) // X,Y input data points #define Y Range(b,1,b,M) #define Z Range(c,1,c,M) // poly approximation Y values #define Err Range(d,1,d,M) // error #define Coef Range($e$,1,$e$,N) // poly coefficients fill X 0, 2/(M-1); a0:e0 = { "X", "Y", "Est", "Err", "Coef" }; Y = { 2+a1*(-2+a1) + (drand()-0.5)/5 }; // y = 2-2*x+x*x + noise {rank,Coef} = llsq("poly",X,Y); Z = { feval("poly",Coef,a1) }; Err = { R[]C[-2]-R[]C[-1] }; err = sqrt(dot(Err,Err)); eval; plot "poly.out" Range(a,1,c,M); format "%10.6f"; format A "%5.2f"; print all; % cat poly.shpoly.html#! /bin/sh SS -t poly -H poly.ss > poly.html printf "set term gif\nset output\nplot 'poly.out' using 1:2 with points notitle,\ 'poly.out' using 1:3 with lines notitle\n" | gnuplot > poly.gif rm poly.out # the points are the original noisy data, # the line is the polynomial approximation to the data% ./poly.sh
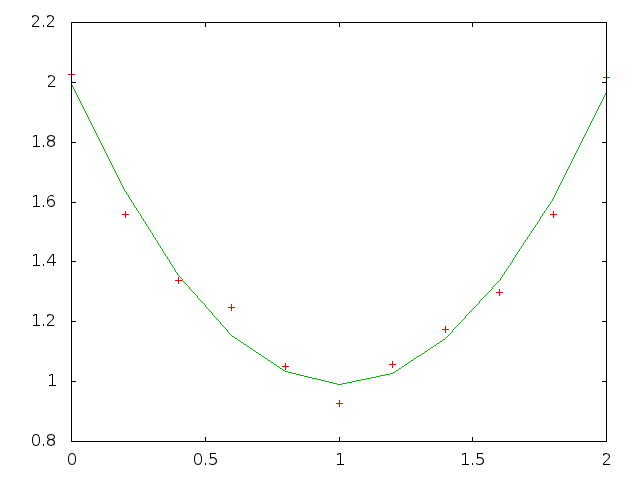
20. search Example
% cat exp.ss // creates noisy exponential data values y = 2*exp(0.5*x), // then finds minimum max-absolute-error approximation z = f1*exp(f2*x) srand 12345; // just to make the docs reproducable, // remove to use default srand(time()) #define M 11 // number of data points #define xCell(c,r) c ## r #define Cell(c,r) xCell(c,r) #define Range(c1,r1,c2,r2) xCell(c1,r1):xCell(c2,r2) #define X Range(a,1,a,M) // X,Y input data points #define Y Range(b,1,b,M) #define Z Range(c,1,c,M) // approximation Y values #define Err Range(d,1,d,M) // absolute error #define Coef f1:f2 // exponential coefficients fill X 0, 4/(M-1); a0:f0 = { "X", "Y", "Est", "Err", "maxErr", "Coef" }; Y = { 2*exp(0.5*a1) + 4*drand()-2 }; // y = 2*exp(0.5*x) + noise Z = { $f$1*exp($f$2*a1) }; Err = { fabs(R[]C[-2]-R[]C[-1]) }; e1 = max(Err); // e1 is the max-absolute-error to be minimized {Coef} = search(e1,3,0.3); // start search with f1=3, f2=0.3 // evaluate Y just once here, // otherwise search() will evaluate it multiple times // eval Y; // eval symbols will evaluate search() which will evaluate everything else // eval symbols; plot "exp.out" Range(a,1,c,M); format "%10.6f"; format A "%5.2f"; print all; % cat exp.shexp.html#! /bin/sh SS -t exp -H exp.ss > exp.html printf "set term gif\nset output\nplot 'exp.out' using 1:2 with points notitle,\ 'exp.out' using 1:3 with lines notitle\n" | gnuplot > exp.gif rm exp.out # the points are the original noisy data, # the line is the exponential approximation to the data% ./exp.sh
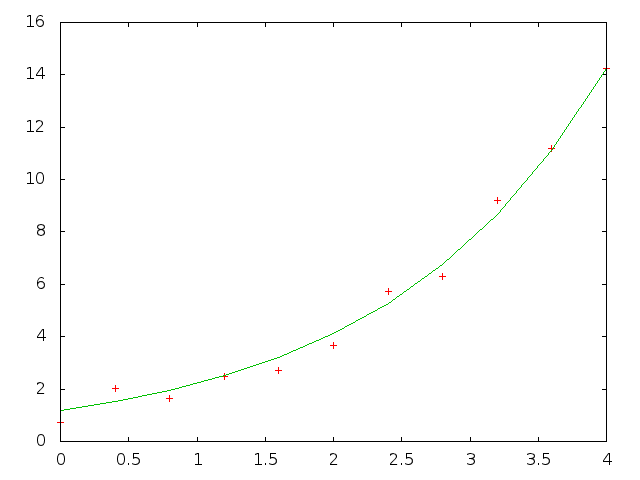
21. Reentrancy
All of the numeric and range functions are reentrant. This means that while a function is executing it may be invoked one or more additional times and the invocations will not interfere with each other.
For example, in sin(2*sin(x))
the first call to the sin() function starts computing 2*...
and to complete the expression sin() is invoked again, as sin(x),
and that result is used in the multiplication by 2 in the first call.
An example of reentrancy using a range function is
max(1+max(a1:a9),2+max(c1:c9)).
Although the range functions llsq and search are also reentrant, they can not be used more than once in the same expression because they return multiple values; they can only be used in multiple assignment statements. However, more than one invocation may be active at the same time, as demonstrated in the following example which minimizes g() to find the value of a3 to use while minimizing f() with respect to a1 and a2:
% cat search.ss // minimize f(a1,a2,a3) with respect to a1,a2 // where a3 minimizes g(a1,a2,a3) given a1,a2 // f = (a1-1)**2 + (a2-2)**2 + a3**2; g = (a3-a1)**2 + (a3-a2)**2; {a1:a2} = search(f,3,4); {a3:a3} = search(g,2); eval; print all; % SS search.ss f = (((A1-1)**2)+((A2-2)**2))+(A3**2) = 1.49991 g = ((A3-A1)**2)+((A3-A2)**2) = 0.501364 $1 = {A1:A2} = search(f,3,4) = 1.49991 $2 = {A3:A3} = search(g,2) = 0.501364 A 1 ($1) 2 ($1) 3 ($2) A 1 0.50 2 1.50 3 1.00This example can easily be analyzed by hand to confirm the above results. Setting the derivative of g() with respect to a3 equal to zero yields a3=(a1+a2)/2. Using that result in f() and setting the derivatives of f() with respect to a1 and a2 to zero yields a1=0.5 and a2=1.5, so then a3=1.0.
22. Keywords and Names
Most keywords are reserved words and can not be used as column names (in the format command) or as variable names (in the symbol table). The only exceptions are the two-letter keywords RC, CR, on, and OR, for convenience since two letters can be used in A0 format to name columns in the default spreadsheet size.OR is case-insensitive when used as an operator or column name, but is case-sensitive when used as a variable name.
Column names can be used as variable names.
The named operators (NOT, AND, XOR, OR, int, long, double), the names of the numeric and range functions, and the names of the commands are all keywords.
stdout, byrows, bycols and the print options constants, formats, formulas, functions, pointers, states, symbols, values are all keywords.
23. Cycles and Convergence
If a cell depends on itself, that forms a cycle and the spreadsheet may not converge when evaluated.Cycles which converge can be used to implement iterative algorithms. For example, the following spreadsheet uses Newton's method to find the square root of x:
% cat sqrt.ss x = 2; a0 = b0 ? b0 : x/2; b0 = (a0+x/a0)/2; format "%20.18g";Since a0 depends on b0, and b0 depends on a0, there is a cycle.
a0 will be set to b0 if b0 is non-zero, otherwise a0 will be set to x/2 to initialize the algorithm. So a0 represents the previous value of b0, and b0 represents the next estimate of the square root. Newton's method converges quickly:
% echo "print all; eval a0:b0 10; print values;" | SS -T sqrt.ss -
x = 2
| A | B | |
|---|---|---|
| 0 | B0 ? B0 : ((x/2)) | (A0+(x/A0))/2 |
| A | B | |
| 0 | 0 | 0 |
| eval: converged after 7 iterations | ||
| A | B | |
| 0 | 1.41421356237309492 | 1.41421356237309492 |
Finite element analysis is another application which requires iteration and can be set up in a spreadsheet. In the following small example, the value of each non-boundary cell is computed as the average of the cell's four nearest neighbors.
% cat cycles.ss // average of 4 nearest neighbors // R1C1:R5C5 = { (R[]C[-1] + R[]C[+1] + R[-1]C[] + R[+1]C[])/4 }; // fill r0c0:r0c6 1, 0; // boundary conditions, fill r1c0:r6c0 1, 0; // 1's top and left fill r1c6:r6c6 0, 0; // 0's right and bottom fill r6c1:r6c5 0, 0; // format "%6.4f"; format RC; % echo "print values; eval 1; eval 1000; print values;" | SS cycles.ss -
0 1 2 3 4 5 6 0 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 2 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 3 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 4 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 5 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 6 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 eval: still changing after 1 iteration eval: converged after 75 iterations 0 1 2 3 4 5 6 0 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1 1.0000 0.9374 0.8747 0.8040 0.7010 0.5000 0.0000 2 1.0000 0.8747 0.7576 0.6404 0.5000 0.2990 0.0000 3 1.0000 0.8040 0.6404 0.5000 0.3596 0.1960 0.0000 4 1.0000 0.7010 0.5000 0.3596 0.2424 0.1253 0.0000 5 1.0000 0.5000 0.2990 0.1960 0.1253 0.0626 0.0000 6 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000The spreadsheet may not converge when using operators ++, --, +=, *=, etc. and the rand, irand, or drand pseudo-random number generator functions, since they produce varying values on each evaluation. However, these operators and functions are still useful, in particular for Monte-Carlo simulations.
The following simple example generates pseudo-random values for a0, with b0 representing the sum, c0 the evaluation count, and d0 the average:
% cat rand.ss srand 34567; // just to make the docs reproducable, // remove to use default srand(time()) a0 = drand(); b0 += a0; d0 = b0/++c0; eval a0:d0 10; print values; % ss < rand.ss
eval: still changing after 10 iterations A B C D 0 0.91 5.37 10.00 0.54
24. Debugging
Debugging of the flex scanner and bison parser is enabled using the -d command-line option.Additional debugging of internal operations is enabled using the debug command. debug off sets the debug level to 0, debug on sets the level to 1, and debug 2 sets the level to 2. Currently, 2 is the highest debug level implemented and produces output for each cell when traversing a range.
A list of the internal functions which implement all
of the operators and functions can be obtained using the
print functions command.
print states; displays the evaluation states and indirect dependencies of the symbols and cells. State 0 indicates that the associated formula has not been evaluated, and state 1 indicates that it has been evaluated. If there is an indirect dependency it is shown in parentheses following the state value.
25. Extensions
Numeric and range functions can be added simply by creating files in the source nf/ and rf/ subdirectories and recompiling. The first line of each function must be a comment specifying the number of return values, number of arguments, and description. The description will appear in the internal help listing and will also be included in the documentation after running make in the doc/ subdirectory.Source example, nf/atan2.c:
/* 1 2 four-quadrant arctangent, atan2(y,x) ~= atan(y/x)
*/
double nf_atan2(const Node *n, const Cell *c)
{
Node *r = Right(n);
return atan2( eval_tree( r, c), eval_tree( r->next, c) );
}
Constants can be added using install_constant() at the end of
main() in parse.so:
install_constant( "HUGE_VAL", HUGE_VAL); install_constant( "DBL_EPSILON", DBL_EPSILON); install_constant( "RAND_MAX", RAND_MAX);
26. Some Implementation Details
soelim (a standard Unix utility) is used to construct the parser flex and bison source files from scan.so, parse.so, and the numeric and range functions defined in the nf/ and rf/ subdirectories. Temporary files used for compilation are created in a tmp/ subdirectory.In the doc/ subdirectory, soelim is also used to construct the documentation from SS.so and temporary files created by running SS to obtain the example outputs and lists of operators, functions, etc. The documentation is processed using sdf (Simple Document Format) to create a single HTML file as well as separate files for each section.
The internal data structures include: Cell, containing row and column numbers and flags for the row or column being fixed or relative; Range, a set of two Cells indicating the start and end of a rectangular region of the spreadsheet; Symbol, containing the name and formula of a symbol; and Node, which can hold a Cell, Range, Symbol, numeric value, string, operator, function code, or pointers to children Nodes in a binary tree. Nodes also contain a next pointer used to form linked-lists of expressions, such as function argument lists.
All operators and functions are stored in a table func indexed by the operator character value or function code. This makes it easy to evaluate operators and functions, i.e. in func.c eval_tree() for Node t:
r = func[t->type]->f( t, ref_cell);Numeric vs. Range functions
All of the numeric functions take a fixed number of arguments; most of the range functions take an indefinite list of arguments, but some of them (dot, feval, and llsq) take a fixed number of arguments. The essential difference between numeric and range functions is that arguments which are ranges are expanded into lists of cells for a numeric function, whereas for a range function they are left as ranges. Internally this difference makes it easier to evaluate numeric functions because they never have to traverse a range.
Range return values for numeric functions are also expanded into lists of cells. For range functions, range return values may or may not be expanded into lists of cells, depending on the function; for stats they are expanded, but for llsq they are not (since llsq needs to know the size of the coefficient return value range).
The following example demonstrates that the range argument of pow (a numeric function) is expanded into a list of cells, whereas the range arguments of stats, llsq, and sum (range functions) are left as ranges. The return values of frexp and stats are expanded into lists of cells, whereas the return value of llsq is not.
% cat numeric_vs_range.ss a0 = pow(b0:c0); {a1:a4} = stats(b0:c0); a5 = sum(b0:c0); {a6,a7:a8} = llsq("poly",b0:c0,b1:c1); {a9:a10} = frexp(sqrt(2)); print symbols formulas; % ss < numeric_vs_range.ss
$1 = {A1,A2,A3,A4} = stats(B0:C0) = 0
$2 = {A6,A7:A8} = llsq("poly",B0:C0,B1:C1) = 0
$3 = {A9,A10} = frexp(sqrt(2)) = 0
A B C
0 pow(B0,C0)
1 ($1)
2 ($1)
3 ($1)
4 ($1)
5 sum(B0:C0)
6 ($2)
7 ($2)
8 ($2)
9 ($3)
10 ($3)