


Next: EM and ML Source
Up: Maximum Likelihood Source Localization
Previous: Introduction
Array Observation Model
We assume the standard narrowband observation model for D far-field sources
impinging on an array of M sensors. Letting 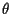 denote the vector
of source location parameters to be estimated,
the array observation is
denote the vector
of source location parameters to be estimated,
the array observation is
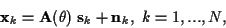 |
(1) |
where  denotes the
denotes the
 vector of signal amplitudes at
time k,
vector of signal amplitudes at
time k,
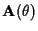 is the
is the
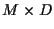 matrix with
(assumed linearly
independent) array response vector columns
matrix with
(assumed linearly
independent) array response vector columns
 for
i=1,...,D.The
for
i=1,...,D.The
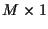 noise vector,
noise vector, 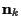 ,
is modeled as a zero-mean,
temporally and spatially white Gaussian process with standard deviation
,
is modeled as a zero-mean,
temporally and spatially white Gaussian process with standard deviation
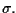 Let
Let
![${\bf X} = [ {\bf x}_1 , {\bf x}_2 , ... , {\bf x}_N ]$](img12.gif) ,
,
![${\bf N} = [ {\bf n}_1 , {\bf n}_2 , ... , {\bf n}_N ]$](img13.gif) ,
and
,
and
![${\bf S} = [ {\bf s}_1 , {\bf s}_2 , ... , {\bf s}_N ]$](img14.gif) .
Then
.
Then
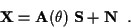 |
(2) |
The complex signal amplitudes in 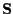 are treated as a
set of ND unknown nuisance or secondary parameters. Our primary interest
is the estimation of the location parameters
are treated as a
set of ND unknown nuisance or secondary parameters. Our primary interest
is the estimation of the location parameters 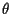 .
With this array observation model and under the CML model assumption, the
probability density function of the
received data (conditioned on
.
With this array observation model and under the CML model assumption, the
probability density function of the
received data (conditioned on 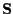 as well as
as well as 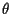 )
is:
)
is:
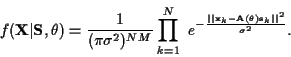 |
(3) |
The basic equations above describe the source localization problem under
consideration, based only on the fact that the additive noise is
spatially/temporally white and Gaussian.
In the succeeding sections, additional
known properties of the random signal amplitudes will be considered, starting
from the most general joint pdf case and proceeding to specific examples of
signal amplitude probability distribution functions.



Next: EM and ML Source
Up: Maximum Likelihood Source Localization
Previous: Introduction
Rick Perry
2000-03-16