


Next: EM Algorithms for Source
Up: Maximum Likelihood Source Localization
Previous: Array Observation Model
For the MAP estimator, we must find 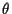 to maximize
to maximize
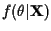 .
Using Bayes rule:
.
Using Bayes rule:
where
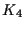 is a constant which takes into account the
effect of
is a constant which takes into account the
effect of
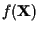 for normalizing the distribution.2
If
for normalizing the distribution.2
If
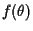 is unknown or assumed to be uniform, then the ML estimator
which maximizes the likelihood function
is unknown or assumed to be uniform, then the ML estimator
which maximizes the likelihood function
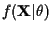 can be used
instead. All of the EM algorithms derived in the subsequent sections here
produce iterative solutions to the ML problem of maximizing
can be used
instead. All of the EM algorithms derived in the subsequent sections here
produce iterative solutions to the ML problem of maximizing
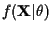 .
But if
.
But if
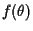 is known and not uniform,
then this could be easily
incorporated into the EM algorithms as an additive term in
the cost function, thus producing a MAP estimator.
The dependence of
is known and not uniform,
then this could be easily
incorporated into the EM algorithms as an additive term in
the cost function, thus producing a MAP estimator.
The dependence of
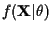 on the random channel coefficients is:
on the random channel coefficients is:
![\begin{displaymath}f({\bf X}\vert \theta ) =
E[f({\bf X}\vert{\bf S}, \theta )] ...
...bf S}} f({\bf X}\vert{\bf S}, \theta )
f({\bf S }) d{\bf S } ,
\end{displaymath}](img28.gif) |
(5) |
where
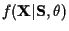 is given by (3).
Evaluating this multidimensional integral and then maximizing the result with
respect to
is given by (3).
Evaluating this multidimensional integral and then maximizing the result with
respect to 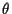 seems to be an intractable problem in general. Yet this
is exactly the problem which the EM algorithms can solve iteratively.
To maximize (5) using EM, define the auxiliary function
[5]:
seems to be an intractable problem in general. Yet this
is exactly the problem which the EM algorithms can solve iteratively.
To maximize (5) using EM, define the auxiliary function
[5]:
where we desire the ML estimate of 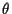 ,
and
,
and 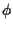 represents the current estimate of
represents the current estimate of 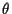 .
In the terminology
of EM,
.
In the terminology
of EM, 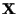 is the observed data,
is the observed data, 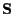 is the hidden data, and
is the hidden data, and
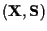 is the complete data.
is the complete data.
The general EM algorithm for this problem is:
- 1.
- Initialize
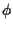 to an estimate of
to an estimate of 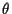 .
.
- 2.
- E-step (Expectation): construct
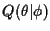
- 3.
- M-step (Maximization): find
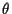 to maximize
to maximize
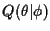
- 4.
- Set
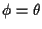 and repeat steps 2 and 3 until converged.
and repeat steps 2 and 3 until converged.
In general, to construct
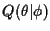 ,
start with
,
start with
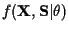 :
:
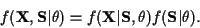 |
(7) |
We can drop the
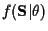 term from this since
term from this since 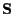 and
and
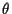 are independent so
are independent so
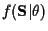 is not a function of
is not a function of
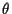 and will not affect the maximization in the M-step.
and will not affect the maximization in the M-step.
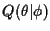 from (6) may then be written as:
from (6) may then be written as:
To evaluate
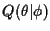 ,
we need
,
we need
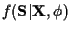 ,
which can be written in terms of the apriori channel coefficient density
function
,
which can be written in terms of the apriori channel coefficient density
function
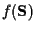 as:
as:
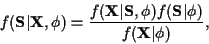 |
(9) |
where the denominator term
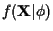 can be treated as a
constant since it simply serves to normalize the distribution, and is not a
function of
can be treated as a
constant since it simply serves to normalize the distribution, and is not a
function of 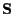 or
or 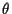 ,
so will not affect the maximization step.
Also,
,
so will not affect the maximization step.
Also,
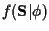 =
=
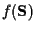 since the signal amplitudes and source locations are independent.
But note that given
since the signal amplitudes and source locations are independent.
But note that given 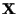 and
and 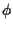 ,
,
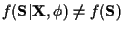 .
Therefore, for
.
Therefore, for
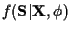 in (8) we may use:
in (8) we may use:
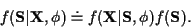 |
(10) |
In the specific cases considered subsequently, we will show that the E-step
reduces to computing sufficient statistics of
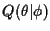 ,
which
are the mean and covariance of
,
which
are the mean and covariance of 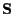 conditioned on
conditioned on 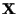 and
and
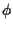 .
This enables the use of an ML-like estimator of
.
This enables the use of an ML-like estimator of 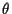 in the
M-step, which employs the sufficient statistics provided in the E-step.
The E-step and M-step formulas will be derived in detail in subsequent
sections for various specific signal amplitude distributions.
in the
M-step, which employs the sufficient statistics provided in the E-step.
The E-step and M-step formulas will be derived in detail in subsequent
sections for various specific signal amplitude distributions.



Next: EM Algorithms for Source
Up: Maximum Likelihood Source Localization
Previous: Array Observation Model
Rick Perry
2000-03-16
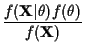
![]() ,
start with
,
start with
![]() :
: