


Next: Hypothesized K-Track Sets
Up: Multitarget Tracking Problem
Previous: Multitarget Tracking Problem
A single hypothesized track is characterized by a measurement vector
or a missed detection for each measurement time. At time n let one
such track, the lth track, be denoted by the measurement-to-track
association vector
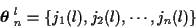 |
(1) |
where the subscript jm (l) is the measurement/missed-detection index at
time m for the lth track. Note that we account for the possibility
of a missed detection by letting jm (l) range from 1 to Jm +1, with
jm (l) = Jm +1 indicating a missed detection.
The vector of measurements for the lth track is
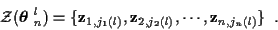 |
(2) |
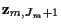 is not an actual measurement, but indicates a missed
detection at time m, and is a notational convenience.
There are
is not an actual measurement, but indicates a missed
detection at time m, and is a notational convenience.
There are
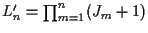 of these hypothesized
tracks:
of these hypothesized
tracks:
 .
Association of the measurements into a single track is the problem of selecting
the best
.
Association of the measurements into a single track is the problem of selecting
the best
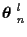 ,
which is equivalent to estimating
the discrete parameter
,
which is equivalent to estimating
the discrete parameter
 .
For a given hypothesized track
.
For a given hypothesized track
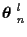 ,
measurement noise is assumed additive, Gaussian and temporally white.
The trajectory and measurements are assumed to
evolve in time according to the state/measurement
equations1
,
measurement noise is assumed additive, Gaussian and temporally white.
The trajectory and measurements are assumed to
evolve in time according to the state/measurement
equations1
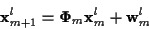 |
(3) |
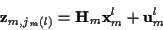 |
(4) |
where at time m and for hypothesized track
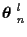 ,
,
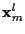 is the state vector, and
is the state vector, and
 and
and 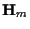 are
the state transition and output matrices respectively. The
are
the state transition and output matrices respectively. The
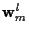 and
and
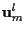 vectors are zero mean, mutually independent, white
and Gaussian with known covariance matrices
vectors are zero mean, mutually independent, white
and Gaussian with known covariance matrices
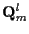 and
and
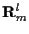 respectively.
A Kalman filter can be applied to this track to smooth the measurements,
to provide minimum variance state vector estimates, and to compute the
innovations for the measurement sequence
respectively.
A Kalman filter can be applied to this track to smooth the measurements,
to provide minimum variance state vector estimates, and to compute the
innovations for the measurement sequence
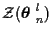 .
For each hypothesis, the measurement innovations sequence
.
For each hypothesis, the measurement innovations sequence
 and corresponding covariance matrices
and corresponding covariance matrices
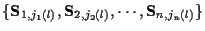 generated using a hypothesis-specific
Kalman filter are to be
used in optimum track estimation. Note that a
generated using a hypothesis-specific
Kalman filter are to be
used in optimum track estimation. Note that a
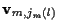 corresponding to
corresponding to
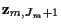 is not an actual
innovation, but is a result of a missed detection at time m, and again
is a notational convenience. In such a case, the Kalman state is just the
predicted state (i.e. no measurement is available to update the state).
is not an actual
innovation, but is a result of a missed detection at time m, and again
is a notational convenience. In such a case, the Kalman state is just the
predicted state (i.e. no measurement is available to update the state).



Next: Hypothesized K-Track Sets
Up: Multitarget Tracking Problem
Previous: Multitarget Tracking Problem
Rick Perry
2000-03-26