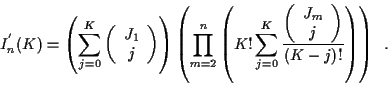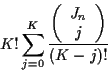Hypothesized K-Track Sets

Now consider a set of K tracks. Assume tracks can not share detections, and again assume missed detections are possible.² It can be shown that the number of hypothesized track sets is³

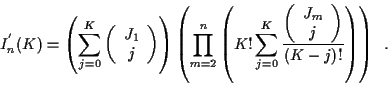$$I_n^{'} (K) = \left( \sum_{j=0}^{K} \left( \begin{array}{c} ... ...J_m} \\ j \end{array} \right)}{(K-j)!} \right) \right) \; \; .$$ (5)

Remember that K is unknown (i.e. it is an unknown variable). For a hypothesized K, let the index i(K) denote the i(K)^thhypothesized K-track set. This K-track set is represented by the i(K)^th set of measurement-to-track associations:

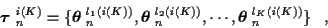$$\mbox{\boldmath$\tau$ }_n^{i(K)} =\{ \mbox{\boldmath$\theta$ ... ...\cdots, \mbox{\boldmath$\theta$ }_n^{l_K (i(K))} \} \; \; \; ,$$ (6)

where the superscript l_k (i(K)) denotes the k^th track of the i(K)^th K-track set. ${\cal Z} ( \mbox{\boldmath$\tau$ }_n^{i(K)} )$ will be used to denote the measurement data corresponding to the i(K)^th K-track set. For known K, Multiple Hypothesis Tracking (MHT) algorithms aim to determine at time n the best from the I_n^' (K) hypothesized track sets. I_n^' (K) grows exponentially with n, with a multiplicative increase of

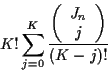$$K! \sum_{j=0}^{K} \frac{\left( \begin{array}{c} {J_n} \\ j \end{array} \right)}{(K-j)!}$$ (7)

hypothesized tracks at each time n. So, I_n^' (K) can be prohibitively large for even moderate values of n, K and numbers of measurements.

Below, for the estimation of K, we introduce a MAP based approach which treats K as an additional variable to be hypothesized over. This increases, relative to MHT with known K, the number of hypotheses to consider. We address this algorithmic issue in Section 4.