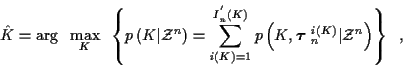Next: MHT Viterbi Algorithm for
Up: MAP Based Estimation of
Previous: Joint Estimation of K
If estimation of K is of primary interest, it can be accomplished without
explicit estimation of
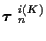 by marginalizing
by marginalizing
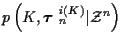 over
the
over
the
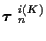 .
Compared to (8),
the resulting estimator,
.
Compared to (8),
the resulting estimator,
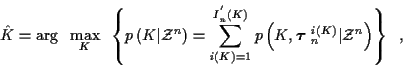 |
(15) |
can have better performance characteristics, particularly for
small number-of-measurement cases.
Rick Perry
2000-03-26