


Next: Trellis Diagram Formulation
Up: Bayesian Track Estimation
Previous: Joint Estimation of K
If estimation of K is of primary interest, it can be estimated without
explicit estimation of
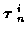 by marginalizing
by marginalizing
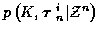 over
over
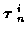 .
Compared to ( 20 ),
the resulting estimator,
.
Compared to ( 20 ),
the resulting estimator,
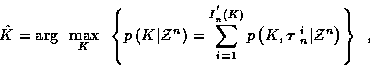 |
(20) |
can have better performance characteristics, which can be better for
small number-of-measurement cases.
has different performance characteristics, which can be better for
small number-of-measurement cases [10].
Rick Perry
1999-03-10
![]() by marginalizing
by marginalizing
![]() over
over
![]() .
Compared to ( 20 ),
the resulting estimator,
.
Compared to ( 20 ),
the resulting estimator,