


Next: Marginalization for Number of
Up: Bayesian Track Estimation
Previous: Estimation of K Tracks
For the estimation of both the number of tracks K and the tracks themselves
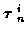 ,
(8) can be considered
a function of unknown K, resulting in the following joint estimation
problem
,
(8) can be considered
a function of unknown K, resulting in the following joint estimation
problem
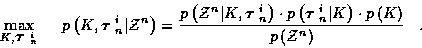 |
(18) |
If we assume that K is uniformly distributed from K=0 to some maximum value
K = Kmax, and that
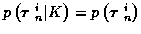 ,
and that
,
and that
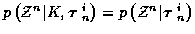 .
This results in the estimator
.
This results in the estimator
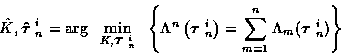 |
(19) |
where all values are as defined for (15),
and now the cost is searched over all
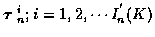 for each
for each
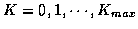 .
(Referring to ( 6 ),
note that the number of candidate track sets for a given K is a function of
K.)
.
(Referring to ( 6 ),
note that the number of candidate track sets for a given K is a function of
K.)
Rick Perry
1999-03-10
![]() ,
(8) can be considered
a function of unknown K, resulting in the following joint estimation
problem
,
(8) can be considered
a function of unknown K, resulting in the following joint estimation
problem