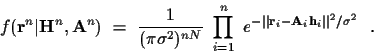Next: MLSE with Gauss-Markov Channels
Up: Multiple User Maximum Likelihood
Previous: Introduction
Multiuser System Model
Here we employ the multiuser, chip-rate sampled, CDMA ISI channel
model described in detail in Wang and Poor [11], extended
to time-varying channels. Index the users as
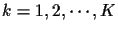 and chips per symbol as
and chips per symbol as
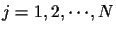 .
The users' signaling
waveforms upon which the user's bits are impressed can be written as
.
The users' signaling
waveforms upon which the user's bits are impressed can be written as
 |
(1) |
where N is the processing gain, ck(j) is the pseudorandom code
assigned to each user and 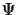 is the normalized chip waveform of
duration Tc=T/N. At the receiver, assume chip-rate sampling over
symbol times
is the normalized chip waveform of
duration Tc=T/N. At the receiver, assume chip-rate sampling over
symbol times
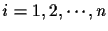 .
The observed data is:
.
The observed data is:
| ri (j) |
= |
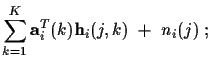 |
(2) |
| |
|
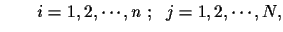 |
|
where the ni (j) are zero-mean Gaussian noise samples
uncorrelated across both i and j with variance 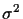 ,
,
 is the
is the
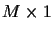 dimensional coefficient
vector for the time-varying FIR channel for the kth user
and jth chip position at symbol time i, M-1 is the memory
depth (in symbols) of the channels, and
dimensional coefficient
vector for the time-varying FIR channel for the kth user
and jth chip position at symbol time i, M-1 is the memory
depth (in symbols) of the channels, and
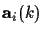 is the
vector of the kth user symbols in the FIR channel
at symbol time i. The
is the
vector of the kth user symbols in the FIR channel
at symbol time i. The
 are unknown
(and time-varying at the symbol rate) and the problem is to
optimally estimate the K users' symbols up to time n.
Defining
are unknown
(and time-varying at the symbol rate) and the problem is to
optimally estimate the K users' symbols up to time n.
Defining
![${\bf a}_i ~ = [ {\bf a}_i^T (1), {\bf a}_i^T (2),
\cdots , {\bf a}_i^T (K) ]^T$](img12.gif) and
and
![${\bf h}_i (j) ~ = [ {\bf h}_i^T (j,1), {\bf h}_i^T (j,2),
\cdots , {\bf h}_i^T (j,K) ]^T$](img13.gif) ,
we have
,
we have
 |
(3) |
The observation over the symbol interval i is
![\begin{displaymath}{\bf r}_i ~ = ~ [ r_i (1) , ~ r_i (2) , \cdots , r_i (N) ]^T
~ ~ ,
\end{displaymath}](img15.gif) |
(4) |
and the observation up to symbol time n is
![\begin{displaymath}{\bf r}^n ~ = ~ [ {\bf r}_1^T , {\bf r}_2^T ,
\cdots , {\bf r}_n^T ]^T ~ .
\end{displaymath}](img16.gif) |
(5) |
Let 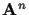 and
and  denote the matrices of,
respectively, all users' symbols and all time-varying FIR
channel coefficients up to time n. (The constructions of
denote the matrices of,
respectively, all users' symbols and all time-varying FIR
channel coefficients up to time n. (The constructions of
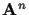 and
and  are not important in this
discussion.) The joint probability density function of
are not important in this
discussion.) The joint probability density function of
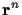 ,
conditioned on
,
conditioned on 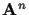 and
and  ,
is
,
is
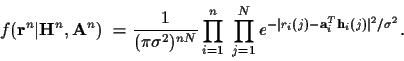 |
(6) |
Define the
 dimensional vector of all channel
coefficients at symbol time i as
dimensional vector of all channel
coefficients at symbol time i as
![\begin{displaymath}{\bf h}_i ~ = ~ [ {\bf h}_i^T (1) , {\bf h}_i^T (2) ,
\cdots , {\bf h}_i^T (N) ]^T
\end{displaymath}](img22.gif) |
(7) |
and consider the
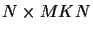 dimensional symbol matrix
at symbol time i
dimensional symbol matrix
at symbol time i
![\begin{displaymath}{\bf A}_i ~ = \left[ \begin{array}{cccccc}
{\bf a}_i^T & {\bf...
...{\bf0}_{1 \times MK} & . & . & {\bf a}_i^T
\end{array} \right]
\end{displaymath}](img24.gif) |
(8) |
where
 is the
is the
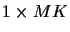 row
vector of zeros. With these we have that
row
vector of zeros. With these we have that
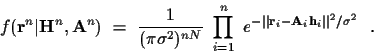 |
(9) |
For the ML estimate of 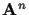 we determine the
we determine the
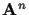 which maximizes
which maximizes
 |
(10) |



Next: MLSE with Gauss-Markov Channels
Up: Multiple User Maximum Likelihood
Previous: Introduction
Rick Perry
2001-11-03


![]() and
and ![]() denote the matrices of,
respectively, all users' symbols and all time-varying FIR
channel coefficients up to time n. (The constructions of
denote the matrices of,
respectively, all users' symbols and all time-varying FIR
channel coefficients up to time n. (The constructions of
![]() and
and ![]() are not important in this
discussion.) The joint probability density function of
are not important in this
discussion.) The joint probability density function of
![]() ,
conditioned on
,
conditioned on ![]() and
and ![]() ,
is
,
is
![\begin{displaymath}{\bf A}_i ~ = \left[ \begin{array}{cccccc}
{\bf a}_i^T & {\bf...
...{\bf0}_{1 \times MK} & . & . & {\bf a}_i^T
\end{array} \right]
\end{displaymath}](img24.gif)