


Next: Reduced Complexity Processing
Up: Multiple User Maximum Likelihood
Previous: Multiuser System Model
MLSE with Gauss-Markov Channels
For a fast time-varying channel with Gauss-Markov fading
parameters, let 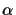 represent a complex first-order
Markov factor such that
represent a complex first-order
Markov factor such that
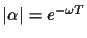 where
T is the symbol period and
where
T is the symbol period and
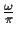 is the
Doppler spread. Let the time-varying channel coefficients
follow a Gauss-Markov distribution such that, at time i,
is the
Doppler spread. Let the time-varying channel coefficients
follow a Gauss-Markov distribution such that, at time i,
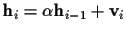 ,
where
,
where 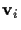 is complex, white, and Gaussian
with zero mean and covariance
is complex, white, and Gaussian
with zero mean and covariance 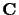 .
In this case,
.
In this case,
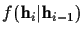 is Gaussian
with mean
is Gaussian
with mean
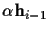 and covariance
and covariance 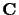 .
.
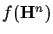 can be written as
can be written as
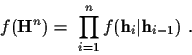 |
(11) |
We assume that the initial channel coefficients are known,
and they are represented as 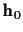 .
Then
.
Then
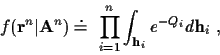 |
(12) |
 .
We can marginalize over the channel coefficient distribution
step by step. The integral over
.
We can marginalize over the channel coefficient distribution
step by step. The integral over  is
is
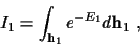 |
(13) |
with
E1 can be reduced, dropping constant terms, to
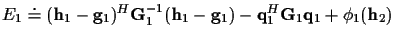 |
|
|
(15) |
with
After integration over  ,
,
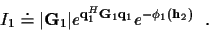 |
(17) |
The term
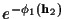 in (17) is
a function of
in (17) is
a function of 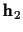 and will be involved in the integral
over
and will be involved in the integral
over 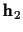 .
The rest of the terms in (17)
are the results after the integration over
.
The rest of the terms in (17)
are the results after the integration over  and are
only decided by the input sequence and will be used to compute
the maximum likelihood probability.
The integral over
and are
only decided by the input sequence and will be used to compute
the maximum likelihood probability.
The integral over 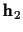 is
is
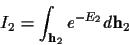 |
(18) |
with
E2 can be reduced, dropping constant terms, to:
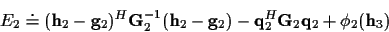 |
(20) |
with
After integration over 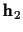 we have:
we have:
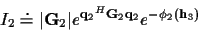 |
(22) |
The last term in (22) will be involved in the
integral over  .
.
The general form of the results after integral over 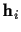 (
i=2,...,n-1) will be
(
i=2,...,n-1) will be
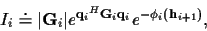 |
(23) |
with
For the integral over 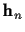 ,
,
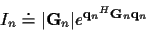 |
(25) |
with
After the integration over all the channel coefficients,
we have the likelihood function
 |
(27) |
If we take the negative natural logarithm of the above equation,
we will obtain the time-recursive form of the cost function
![\begin{displaymath}- \log f({\bf r^n}\vert{\bf A^n}) \doteq ~ - ~
\sum_{i=1}^n \...
...i}^{H} {\bf G}_i {\bf q}_i}+
\log \vert{\bf G}_i\vert \right].
\end{displaymath}](img83.gif) |
(28) |
From the expressions of  and
and 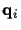 we know
the transition costs depend on all the previous states, so
the standard Viterbi algorithm cannot be applied here.
The optimum results can only be obtained
by exhaustive search.
we know
the transition costs depend on all the previous states, so
the standard Viterbi algorithm cannot be applied here.
The optimum results can only be obtained
by exhaustive search.



Next: Reduced Complexity Processing
Up: Multiple User Maximum Likelihood
Previous: Multiuser System Model
Rick Perry
2001-11-03
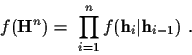
![]() (
i=2,...,n-1) will be
(
i=2,...,n-1) will be
![]() ,
,
![]() and
and ![]() we know
the transition costs depend on all the previous states, so
the standard Viterbi algorithm cannot be applied here.
The optimum results can only be obtained
by exhaustive search.
we know
the transition costs depend on all the previous states, so
the standard Viterbi algorithm cannot be applied here.
The optimum results can only be obtained
by exhaustive search.