


Next: EM and ML Sequence
Up: EM Algorithms for Sequence
Previous: Introduction
Communication System Model
In the discrete-time FIR model of a noisy communications channel
with inter-symbol interference, for a block of N received data values,
the complex received data rk at time k is given by:
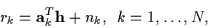 |
(1) |
where
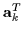 is a complex row vector containing transmitted data
{
is a complex row vector containing transmitted data
{
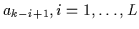 }, L is the FIR channel length,
}, L is the FIR channel length,
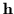 is a complex column vector containing the channel impulse response coefficients
(which are unknown), and
nk is the white Gaussian complex noise at time k with variance
is a complex column vector containing the channel impulse response coefficients
(which are unknown), and
nk is the white Gaussian complex noise at time k with variance 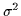 .
For
.
For 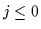 , the transmitted data aj may be either known (e.g. all 0's),
unknown, or estimated with some associated probabilities from the end of
a previous data block.
Using matrix-vector notation, the above equations can then be expressed
more simply as:
, the transmitted data aj may be either known (e.g. all 0's),
unknown, or estimated with some associated probabilities from the end of
a previous data block.
Using matrix-vector notation, the above equations can then be expressed
more simply as:
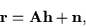 |
(2) |
and
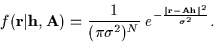 |
(3) |



Next: EM and ML Sequence
Up: EM Algorithms for Sequence
Previous: Introduction
Rick Perry
1999-10-28