


Next: EM Algorithms
Up: Direct and EM-based MAP Channels
Previous: Data Model
MAP Sequence Estimation
Here we summarize results from [2].
For channel coefficients which are
independent over time,
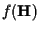 can be expressed as
can be expressed as
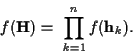 |
(4) |
If
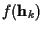 is Gaussian with mean
is Gaussian with mean 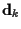 and covariance
and covariance
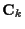 ,
then
,
then
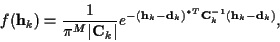 |
(5) |
where * denotes conjugate. We assume that 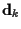 and
and 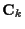 are known.
Substituting (2) and (4) into
(3), taking
the negative
natural logarithm of the integration result and ignoring the terms that are
irrelevant to
the minimization, we
obtain:
are known.
Substituting (2) and (4) into
(3), taking
the negative
natural logarithm of the integration result and ignoring the terms that are
irrelevant to
the minimization, we
obtain:
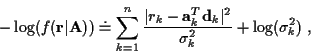 |
(6) |
where
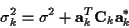 |
(7) |
and  denotes equivalent for optimization purposes.
The time-recursive form for (6) is obvious, and since
the incremental cost only depends on the state transition at the current time,
the Viterbi algorithm can be used directly as an efficient, exact
MAP (optimum) algorithm.
denotes equivalent for optimization purposes.
The time-recursive form for (6) is obvious, and since
the incremental cost only depends on the state transition at the current time,
the Viterbi algorithm can be used directly as an efficient, exact
MAP (optimum) algorithm.
For a fast time-varying channel with Gauss-Markov fading parameters, the
optimum solution is derived in [2] where a
computationally effective suboptimum algorithm based on PSP and GVA
is also proposed.
Concerning PSP, for each trellis survivor path the quantities involved in the
transition cost are computed by channel model aided estimation as dictated
by the MAP formulation. As per GVA, at each state of
each stage of the trellis, we keep 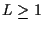 survivors.
We show that for reasonable L the algorithm approaches
optimum results.
survivors.
We show that for reasonable L the algorithm approaches
optimum results.



Next: EM Algorithms
Up: Direct and EM-based MAP Channels
Previous: Data Model
Rick Perry
2001-04-06
![]() can be expressed as
can be expressed as
![]() survivors.
We show that for reasonable L the algorithm approaches
optimum results.
survivors.
We show that for reasonable L the algorithm approaches
optimum results.