


Next: Summary
Up: Direct and EM-based MAP Channels
Previous: EM Algorithms
Numerical Results
Figures 2 and 3 show typical results from
Monte-Carlo simulations using Gauss-Markov channel coefficients.
Figure 2 shows the direct MAP
PSP GVA algorithm for a Gauss-Markov channel with zero mean
and covariance
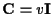 with v = 0.001. This illustrates that
even for small L near optimum results can be obtained.
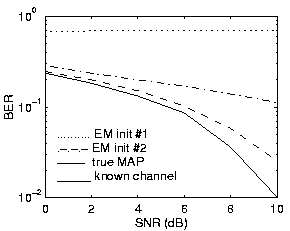
Figure 3 is a comparison of EM and direct MAP,
using parameters
n = 10, M = 3,
with v = 0.001. This illustrates that
even for small L near optimum results can be obtained.
Figure 3 is a comparison of EM and direct MAP,
using parameters
n = 10, M = 3,
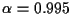 ,
v = 0.01,
,
v = 0.01,
 ,
and
,
and
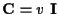 .
The direct MAP BER results were obtained by an exhaustive
search of the ML cost function. Two different initializations
for the EM algorithm were used, both of which produce unreasonably large BER.
Initialization 1 (init #1) used known
.
The direct MAP BER results were obtained by an exhaustive
search of the ML cost function. Two different initializations
for the EM algorithm were used, both of which produce unreasonably large BER.
Initialization 1 (init #1) used known 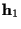 and
and
 .
Initialization 2
used known
.
Initialization 2
used known 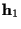 and
0's for the initial symbol estimates. Other researchers have found
that EM initialization can be improved using pilot bits.
We have performed many simulations which confirm that EM with
proper initialization can provide MAP results.
and
0's for the initial symbol estimates. Other researchers have found
that EM initialization can be improved using pilot bits.
We have performed many simulations which confirm that EM with
proper initialization can provide MAP results.
Figure 2:
BER for Gauss-Markov PSP
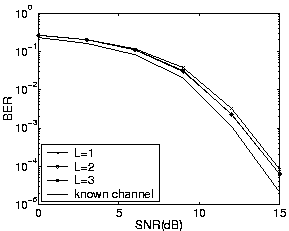 |
Figure 3:
BER for different Gauss-Markov EM initializations
 |



Next: Summary
Up: Direct and EM-based MAP Channels
Previous: EM Algorithms
Rick Perry
2001-04-06
