


Next: Number-of-Track Estimation
Up: MHT Viterbi Algorithm for
Previous: Trellis Diagram Formulation
Based on the trellis diagram problem formulation described above, we now
describe a multitarget track estimation algorithm which provides a list of
L track sets. The
algorithm is sequential, self-initiating and can handle false alarms and
missed detections. In this subsection we assume K is known and constant,
and we are interested in identifying the MAP estimate of the K-track set.
The problem is to find the lowest cost path through the trellis described
in Subsection 4.1.
For the MAP estimation problem considered here, the need for
(infinite memory) Kalman filters for each hypothesized track precludes the
use of the Viterbi algorithm, so that to solve the problem at
time n an exhaustive search of all
In' (K) paths through the trellis
appears necessary. At any stage n in the trellis, this requires that we
consider all paths into each state at stage n-1, each extended to all
states at stage n. That is, the
In-1' (K) paths into stage n-1
must be extended to the
In' (K) paths into stage n, even though
the costs of some of these paths will indicate that the corresponding
K-track sets are highly unlikely. We propose to keep, at each stage in
the trellis, a ``list'' of only the best (lowest cost) L paths to each
state, where L is selected to assure that no feasible paths are
pruned6. Generically, the list Viterbi algorithm
[10] does this.
The multitarget tracking algorithm we employ [7]
incorporates the list Viterbi
algorithm, along with the K-track trellis formulation of the multitarget
tracking problem [9], and MAP cost computation based on Kalman
filter innovations and prior tract set probabilities. The algorithm
determines a list of L feasible K-tracks sets as a list of L paths
through the measurement set trellis.
Algorithm
- 1)
- Setup:
For each time
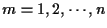 ,
allocate arrays of size Mm-by-L for the
predecessor state indices, predecessor state L-best indices,
permutation number of the current state measurement indices to track
associations, and current total minimum negative log costs. Allocate
Kalman filters for each track in each L-best sets of tracks for each state.
,
allocate arrays of size Mm-by-L for the
predecessor state indices, predecessor state L-best indices,
permutation number of the current state measurement indices to track
associations, and current total minimum negative log costs. Allocate
Kalman filters for each track in each L-best sets of tracks for each state.
- 2)
- Initialization:
For
 ,
the current costs are set using
the a priori
probabilities, since no Kalman filter innovations are available
initially. The Kalman filters are initialized using the available
measurements for time m=1, and using predicted values for time m=2.
,
the current costs are set using
the a priori
probabilities, since no Kalman filter innovations are available
initially. The Kalman filters are initialized using the available
measurements for time m=1, and using predicted values for time m=2.
- 3)
- Iteration:
For each time
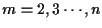 ,
and for each state
,
and for each state
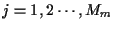
- 3.1)
- Add incremental costs (17)
from the L-best of each previous state to the total previous costs, and
temporarily store these hypothesized new costs.
- 3.2)
- Implement additional hypothesis merging and pruning as discussed below.
- 3.3)
- Select the L-best of the hypothesized new
costs7
and update the associated Kalman filters.
- 4)
- Results: Output the final L-best sets of tracks.
Although the algorithm is described above in block data form, it is
time-sequential, and at any time during the iterations can produce current
estimates of the best tracks.
Additional Hypothesis Merging and Pruning
The list-Viterbi implementation prunes the number of hypotheses out of
stage m to
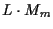 .
The value of L required to achieve a
certain level of performance can be reduced by merging similar paths
into a state prior to pruning the number of paths to L. This way,
the list of L will contain diverse hypotheses, which is the objective
(i.e. we want to keep some less-likely, significantly different hypotheses
on the chance that they will become part of more likely hypotheses later in
time).
In order to merge similar paths, a criteria must be established to
determine whether paths are similar enough to be merged. The criteria
used in our simulation code follows. Tracks are merged if:
.
The value of L required to achieve a
certain level of performance can be reduced by merging similar paths
into a state prior to pruning the number of paths to L. This way,
the list of L will contain diverse hypotheses, which is the objective
(i.e. we want to keep some less-likely, significantly different hypotheses
on the chance that they will become part of more likely hypotheses later in
time).
In order to merge similar paths, a criteria must be established to
determine whether paths are similar enough to be merged. The criteria
used in our simulation code follows. Tracks are merged if:
- 1.
- they end on the same trellis state and state permutation,
or if some of the K tracks end in a sequence of missed target events and
the last actual measurements used for these tracks (at some previous trellis
stage) are the same while the rest of the K tracks have common
measurements back to the this previous stage; and
- 2.
- the trellis states used for the track sets coincide for at least two
stage indices, and differ for no more than one stage index.
At each trellis state, the similar paths are first identified. For each
set of similar paths, the paths are
probabilistically averaged [3],
i.e. the associated Kalman filter states
are averaged, weighted by their normalized probabilities. The resulting
averaged Kalman states then replace the states for the most likely path in
the set, and the other similar paths are pruned.



Next: Number-of-Track Estimation
Up: MHT Viterbi Algorithm for
Previous: Trellis Diagram Formulation
Rick Perry
2000-03-26