


Next: The MHT Viterbi Algorithm
Up: MHT Viterbi Algorithm for
Previous: MHT Viterbi Algorithm for
To derive an equivalent cost from which a time recursive trellis structure
representation can be developed, take the negative natural log of
(14). The following equivalent cost is obtained:
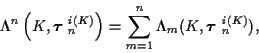 |
(16) |
where the time m incremental cost is
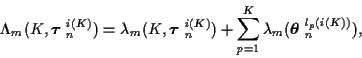 |
(17) |
where
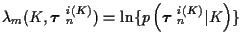 and the pth track incremental cost at time m is
and the pth track incremental cost at time m is
For now, assume that K is known.
Assume that tracks can not share detections,
and that missed detections (as many as K at time m) are possible.
With these assumptions we define a trellis representation of all hypothesized
K track sets. This trellis is depicted in Figure 1.
At each stage (time), each state represents a set of K measurements
and/or missed detections. (This is the trellis proposed by Wolf,
et al. [9])
For stage m with Jm measurements, there are
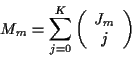 |
(19) |
states (nodes).
A branch is a connection from a state at some time m-1 to one at
time m. Each branch from stage m-1 to m has a set of
K !/(Kmax - Jm + Fmi(K) )!permutations associated with it, specifying the possible orders in which
the K measurements and/or missed detections represented by the state at
stage m are used.5
Each permutation corresponds to one or more hypothesized K-track set.
Each incremental cost assigned to a branch is the sum of a prior cost
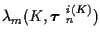 and the
costs of the K hypothesized tracks. So, for
hypothesized K-track set
and the
costs of the K hypothesized tracks. So, for
hypothesized K-track set
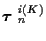 ,
the branch cost from
stage m-1 to m is
,
the branch cost from
stage m-1 to m is
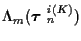 .
Note that the problem of identifying the best K-track set is now one
of finding the minimum-cost path through this trellis.
.
Note that the problem of identifying the best K-track set is now one
of finding the minimum-cost path through this trellis.
![\begin{figure}% latex2html id marker 382
\begin{center}
\begin{tabular}{c}
\ps...
...{center} \caption[gentrellis]
{Trellis Diagram for general $K$ .}
\end{figure}](img59.gif)



Next: The MHT Viterbi Algorithm
Up: MHT Viterbi Algorithm for
Previous: MHT Viterbi Algorithm for
Rick Perry
2000-03-26
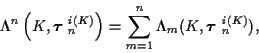
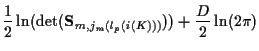
![]() and the
costs of the K hypothesized tracks. So, for
hypothesized K-track set
and the
costs of the K hypothesized tracks. So, for
hypothesized K-track set
![]() ,
the branch cost from
stage m-1 to m is
,
the branch cost from
stage m-1 to m is
![]() .
Note that the problem of identifying the best K-track set is now one
of finding the minimum-cost path through this trellis.
.
Note that the problem of identifying the best K-track set is now one
of finding the minimum-cost path through this trellis.