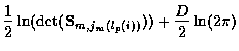Next: Joint Estimation of K
Up: Bayesian Track Estimation
Previous: Bayesian Track Estimation
Using a Bayesian formulation which
incorporates prior track set probabilities, at time n we have the following
optimization problem for the
selection from
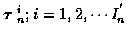
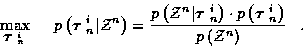 |
(7) |
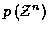 is a normalizing factor which
serves to make the possible values of
is a normalizing factor which
serves to make the possible values of
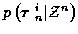 sum to
unity, and can be ignored since it is independent of
sum to
unity, and can be ignored since it is independent of
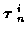 .
.
 is the apriori probability
of the set of tracks, and is derived from the known probability of missed
detections and the false alarm rate. Letting
Jm = Tmi + Fmi, where
Tmi is the number of measurement vectors at time m used in the Ktrack set
is the apriori probability
of the set of tracks, and is derived from the known probability of missed
detections and the false alarm rate. Letting
Jm = Tmi + Fmi, where
Tmi is the number of measurement vectors at time m used in the Ktrack set
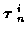 and Fmi is the number of assumed
false alarms, we have that
and Fmi is the number of assumed
false alarms, we have that
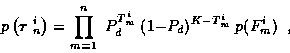 |
(8) |
where
p( Fmi ) is the Poisson distributed probability of Fmi
false alarms.
 is the joint probability density function of the measurements
is the joint probability density function of the measurements
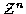 conditioned on the track set
conditioned on the track set
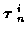 .
For a given
.
For a given
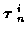 ,
we can
partition
,
we can
partition
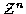 into the data associated with the
tracks,
into the data associated with the
tracks,
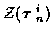 ,
and data associated with
false alarms,
,
and data associated with
false alarms,
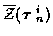 .
We then have
.
We then have
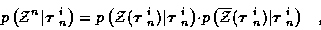 |
(9) |
where, under the assumption that false alarms are uniformly distributed
over the surveillance volume Y,
 |
(10) |
In terms of the Kalman filter generated measurement innovations, for the
track measurements,
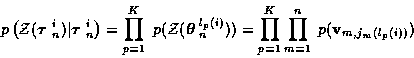 |
(11) |
where for each track p the product over m does not include any missed
detections since as noted earlier measurements and innovations for
missed detections don't exist. Keeping this in mind,
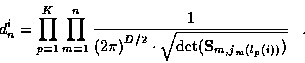 |
(12) |
The Bayesian cost for estimating the best K tracks is described by
(8),
along with (9), (11),
(13) and (14).
To derive an equivalent cost from which a time recursive trellis structure
representation can be derived, take the negative natural log of
(8),
ignoring
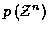 .
For the ith track set, the following equivalent Bayesian optimization
problem is obtained:
.
For the ith track set, the following equivalent Bayesian optimization
problem is obtained:
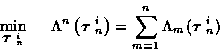 |
(13) |
where the time incremental cost is
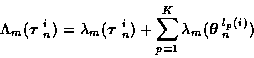 |
(14) |
with
and the pth track incremental cost at time m is
Although from (15), the time recursion
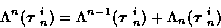 |
(17) |
can be formed, to solve this Bayesian problem directly, at time n
In' incremental costs must be computed. In the following sections
we develop an algorithmic approach which reduces this computational
requirement.



Next: Joint Estimation of K
Up: Bayesian Track Estimation
Previous: Bayesian Track Estimation
Rick Perry
1999-03-10
![]()
![]() is the joint probability density function of the measurements
is the joint probability density function of the measurements
![]() conditioned on the track set
conditioned on the track set
![]() .
For a given
.
For a given
![]() ,
we can
partition
,
we can
partition
![]() into the data associated with the
tracks,
into the data associated with the
tracks,
![]() ,
and data associated with
false alarms,
,
and data associated with
false alarms,
![]() .
We then have
.
We then have
![]() .
For the ith track set, the following equivalent Bayesian optimization
problem is obtained:
.
For the ith track set, the following equivalent Bayesian optimization
problem is obtained: