


Next: Bibliography
Department of Electrical and Computer Engineering
Villanova University
Villanova, PA 19085
Multitarget List Viterbi Tracking Algorithm
Richard Perry - Anand Vaddiraju - Kevin Buckley
perry(anand, buckley)@ece.vill.edu
Abstract:
In this paper we present an approach to multitarget tracking algorithm
development. The approach is based on a trellis diagram which depicts the
possible progressions of sequences of location measurements over time.
Resulting algorithms are sequential and very flexible in that the
approach can handle multiple tracks, track initiation, missed detections,
false alarms, and various performance cost functions, while managing
computation cost by pruning based on track feasibility. The output of a
resulting algorithm can be either a single best set of K tracks, or
a list of L best sets of K tracks. The latter is useful, for example,
in data fusion where information from other platforms can be used to
select one set from the list.
1. Introduction
Multitarget tracking is an important and challenging problem in radar signal
processing [1] which is receiving renewed attention within the
context of multi-platform system integration (i.e. data fusion).
Starting from a time evolving set of noisy detected and
false alarm target location/velocity estimates, the problem is to
associate the detections over time to form multiple target tracks.
For example, maximum likelihood (ML) based data association algorithms have
been developed based on track splitting [2], and integer programming
[3]. In [1] and [4] algorithms based on a
Bayesian formulation have been proposed.
In [5], a K-path extension of the Viterbi algorithm
is used to find the best K tracks according to a deterministic energy cost
function. These approaches identify a set of
multiple tracks but do not directly address the possibility that there
may be alternative yet reasonable sets of tracks that fit the data nearly as
well in the sense optimized to. Such an alternative set of tracks could
be the correct set, which in a multiplatform/data-fusion scenario could be
determinable with post processing given additional information that would
become available.
In this paper we introduce an approach to algorithm development
which provides a ranked list of multiple tracks, along with their
accompanying costs. The approach is based on a trellis diagram which
depicts the possible progressions of sequences of location measurements
over time. The processing structure can implement a variety of costs,
including ML, Bayesian and deterministic energy. We will focus
on maximizing the multitrack likelihood. In this case, trellis branch costs
are computed from track innovation processes generated by Kalman filters.
Because of the nature of the relationship between measurements and
innovations, the Viterbi algorithm can not be used to prune (eliminate from
consideration) trellis paths. This is because neither the track innovation
nor state processes are Markov. However, a generalization of the Viterbi
algorithm termed the list Viterbi algorithm can be used to prune, at each
stage and state, all but a subset of tracks called the feasibility tracks.
Below we first describe the tracking problem using an ML
formulation. We then describe the trellis diagram based approach, and
present a K-track list Viterbi algorithm for ML track
estimation. We illustrate this algorithm with a numerical example.
2. Problem Formulation
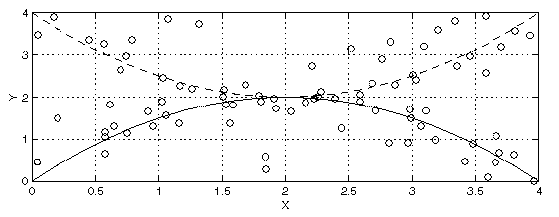
Figure 1 illustrates a tracking scenario with measurements taken over time,
plotted as 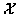 vs.
vs. 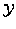 location coordinates. Two parabolic target tracks
are shown. For each target,
location coordinates. Two parabolic target tracks
are shown. For each target, 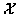 increases over time. Detections at
each time instant consist of noisy measurements of the two targets, along
with two false alarms. In general, for detection k at time n, the measurement vector defined as
increases over time. Detections at
each time instant consist of noisy measurements of the two targets, along
with two false alarms. In general, for detection k at time n, the measurement vector defined as
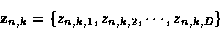 |
(1) |
may consist of 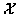 and
and 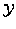 coordinates, range and azimuth, velocity parameters etc.
The problem we address is to associate detections over time to estimate a set of K target tracks.
coordinates, range and azimuth, velocity parameters etc.
The problem we address is to associate detections over time to estimate a set of K target tracks.
Figure 1:
True tracks and noisy measurements with clutter
 |
Assume that at time index n there are Jn target detections, each of
which consists of a set of estimated location/velocity parameters
arranged in a measurement vector. We assume that K targets are
present. Each detection may be a true target detection or a false alarm.
In this paper we assume that for each target and each time n the probability
of detection PD = 11.
A candidate track consists of a set of measurements, one taken for each time.
At time n, there are
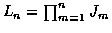 candidate tracks.
Let
candidate tracks.
Let
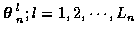 represent these, i.e.
represent these, i.e.
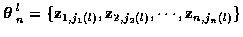 where jm (l) indicates the measurement taken from
time m for track l, and
where jm (l) indicates the measurement taken from
time m for track l, and
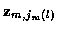 is the jm (l)measurement vector at time m. So the candidate track l at time n is
characterized by
is the jm (l)measurement vector at time m. So the candidate track l at time n is
characterized by
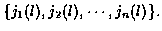
Measurement noise is assumed additive, Gaussian and temporally white.
For candidate track l the trajectory and measurements are assumed to evolve
in time according to the state/measurement equations
2
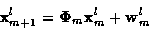 |
(2) |
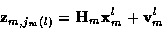 |
(3) |
where at time m and for candidate track l,
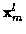 is the state
vector, and
is the state
vector, and
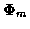 and
and 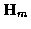 are the state transition and
output matrices respectively. The
are the state transition and
output matrices respectively. The
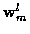 and
and
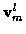 vectors
are zero mean, mutually independent, white and Gaussian with known covariance
matrices
vectors
are zero mean, mutually independent, white and Gaussian with known covariance
matrices 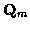 and
and 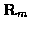 respectively.
respectively.
2.1 Single Track Problem
For the single track (K=1) case, given the lth candidate track is
correct, the probability density function of the track measurements
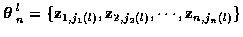 is
is
where
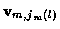 is the innovation of
is the innovation of
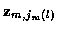 ,
,
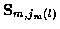 is its covariance matrix, and cn is a track
independent constant. The
is its covariance matrix, and cn is a track
independent constant. The
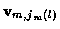 and
and
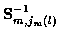 are
generated by running a Kalman filter on the lth candidate track
measurement sequence
are
generated by running a Kalman filter on the lth candidate track
measurement sequence
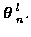 The ML track estimate,
The ML track estimate,
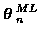 ,
is the
solution to the problem:
,
is the
solution to the problem:
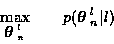 |
(5) |
which is equivalent to minimizing the -log likelihood:
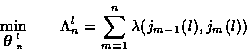 |
(6) |
where
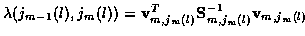 is the incremental cost
associated with going, in track
is the incremental cost
associated with going, in track
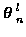 ,
from measurement
,
from measurement
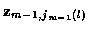 at time m-1 to measurement
at time m-1 to measurement
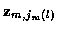 at time m. To directly solve this ML problem, for each time n,
Eq (4) must be evaluated for all Ln candidate tracks.
at time m. To directly solve this ML problem, for each time n,
Eq (4) must be evaluated for all Ln candidate tracks.
2.2 K Track Problem
For the K track case, the number of candidate sets of K non-intersecting tracks at time n is In, where
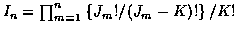 .
Let the ith candidate K-track set be
.
Let the ith candidate K-track set be
 Given that
track set i is true, the probability density function of the combined
Given that
track set i is true, the probability density function of the combined
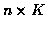 track measurements in
track measurements in
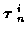 is
is
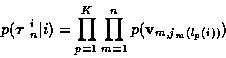 |
(7) |
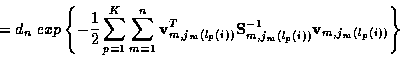 |
(8) |
where dn is a constant independent of track set i.
Generalizing the single track ML problem, the ML K-track estimate,
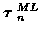 ,
is the solution to the problem:
,
is the solution to the problem:
 |
(9) |
To directly solve this problem, for each time n,
Eq (8) must be evaluated for all In candidate K-tracks.
2.3 Trellis Diagram Representation
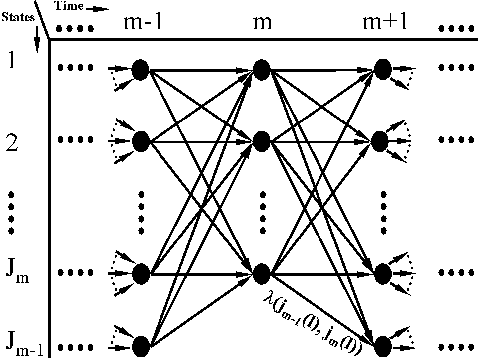
Consider the trellis diagram in Figure 2 which depicts the possible
progressions of sequences of location measurements over time for K=1. Each stage of
the trellis corresponds to a measurement time. For K=1, at the mthstage, each of the Jm measurements corresponds to a state. A branch is a
connection from a state at stage m-1 to another state at stage m.
At time n, the Ln candidate tracks
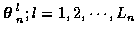 correspond to the Ln possible paths through the trellis from stage 1 to n.
For each track, we assign an incremental cost to each branch. For example,
for the lth candidate track
correspond to the Ln possible paths through the trellis from stage 1 to n.
For each track, we assign an incremental cost to each branch. For example,
for the lth candidate track
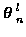 ,
the branch cost from
stage m-1 to m (i.e. from state
jm-1 (l) to jm (l)) is
,
the branch cost from
stage m-1 to m (i.e. from state
jm-1 (l) to jm (l)) is
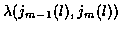 .
It is important to note that since for each candidate track a Kalman
filter (which has memory back to the 1st stage through the Kalman states)
is being used to compute the incremental costs, the cost associated with
a branch depends on what track is being considered. That is, each branch has
multiple costs assigned to it, one for each track through it.
The cost of the path
.
It is important to note that since for each candidate track a Kalman
filter (which has memory back to the 1st stage through the Kalman states)
is being used to compute the incremental costs, the cost associated with
a branch depends on what track is being considered. That is, each branch has
multiple costs assigned to it, one for each track through it.
The cost of the path
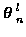 is the sum of its branch costs.
The ML track estimation problem is now one of finding the minimum-cost path
through this trellis.
is the sum of its branch costs.
The ML track estimation problem is now one of finding the minimum-cost path
through this trellis.
Figure 2:
Trellis diagram for K = 1
 |
For K track estimation, each state of the trellis in Figure 2 is
a set of K measurements. So, for stage m with Jm measurements,
there are
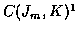 states.
Now for each candidate K-track set, the incremental cost assigned to a
branch is the sum of the costs of K candidate tracks. So, for
candidate K-track set
states.
Now for each candidate K-track set, the incremental cost assigned to a
branch is the sum of the costs of K candidate tracks. So, for
candidate K-track set
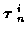 ,
the branch cost from
stage m-1 to m is
,
the branch cost from
stage m-1 to m is
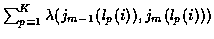 .
As with the K=1 case, the ML K-track estimation problem is now one of
finding the minimum-cost path through this trellis.
.
As with the K=1 case, the ML K-track estimation problem is now one of
finding the minimum-cost path through this trellis.
3. A List Viterbi Tracking Algorithm
Based on the trellis diagram problem formulation described above, we now describe a multitarget ML track estimation algorithm which provides a list of L best K-tracks.
The algorithm is sequential, self-initiating and can handle false alarms.
Although the algorithm can be modified to compensate for missed
detections by employing extra ``absent return'' trellis states, as described
here, at each time the algorithm must assign an available measurement (be it
an actual detection or false alarm) to each track. In this section a
K-track algorithm is described, so that K=1 is treated within this context.
The ML tracking algorithm described in Section 2 would, if solved directly,
be computationally prohibitive for large n and even moderate values of
K and the Jm 's. Approaches have been proposed to reduce the number of
candidate tracks based on feasible tracks [1,2,3].
Effectively, at each time m, the feasible tracks approach eliminates
from further consideration the candidate tracks that have too large (i.e. too unlikely) incremental costs at that time. Here we take a similar
approach, and implement it within the trellis problem formulation.
The problem is to find the lowest cost path through
the trellis. The Viterbi algorithm [7] can be used to sequentially
prune the paths through the trellis for certain ML optimization problems
(as well as for some other problems).
At any stage in the trellis, it keeps only
one path to each state. So it is only applicable to problems for which
all other paths can not be optimum. It has been used extensively in
digital communication and other application problems for which the sequence
can be modeled as a Markov process. It has also been proposed for multitarget
tracking based on a deterministic energy cost [5], where the
incremental path costs from a state jm-1 at stage m-1 to a state
jm at stage m is a function of only the jm-1 and jm measurements.
In general, multitarget tracking problems, couched in a trellis framework, can
not be solved using the Viterbi algorithm. For the ML problem considered
here, the need for (infinite memory) Kalman filters for each candidate track
precludes its use, so that to solve the ML problem at time n an exhaustive
search of all Ln paths through the trellis appears necessary. At any
stage n in the trellis this requires that we consider all paths into each
state at stage n-1, each extended to all states at stage n. That is, the
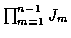 paths into stage n-1 must be extended to the
paths into stage n-1 must be extended to the
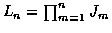 paths into stage n, even though the costs of
some of these paths will indicate that the corresponding K-track sets are
highly unlikely. Alternatively, we propose to keep, at each stage in the
trellis, a ``list'' of only the best (lowest cost) L paths to each state,
where L is selected to assure that no feasible paths are pruned
3.
paths into stage n, even though the costs of
some of these paths will indicate that the corresponding K-track sets are
highly unlikely. Alternatively, we propose to keep, at each stage in the
trellis, a ``list'' of only the best (lowest cost) L paths to each state,
where L is selected to assure that no feasible paths are pruned
3.
Generically, the list Viterbi algorithm [6] does this. The
multitarget tracking algorithm we propose incorporates the list Viterbi
algorithm, along with the K-track trellis formulation of the multitarget
tracking problem [5], and ML cost computation based on Kalman filter
innovations [2]. The algorithm determines a list of L feasible
K-tracks sets as a list of L paths through the trellis. In general,
paths are evaluated according to a defined cost function, where the
incremental costs in progressing from stage to stage are computed as branch
costs from states to states.
3.1 A Simple Illustrative Example
Here we will apply the algorithm to a simple case consisting of K = 2targets, with measurements spanning 3 instants of time, and find the L = 2best sets of tracks.
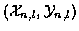 are the
are the
 coordinates of the lthtarget at time n. Table 1(a) shows these coordinates.
We assume the measurement vector
coordinates of the lthtarget at time n. Table 1(a) shows these coordinates.
We assume the measurement vector
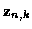 consists of
consists of 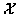 and
and
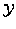 coordinates only. For the purpose of illustration, we add one
clutter/false-alarm measurement at each instant, and assume no measurement noise. Therefore, there are
J = 3 measurements per time
instant - two actual and one clutter. Table 1(b) shows these
measurements.
coordinates only. For the purpose of illustration, we add one
clutter/false-alarm measurement at each instant, and assume no measurement noise. Therefore, there are
J = 3 measurements per time
instant - two actual and one clutter. Table 1(b) shows these
measurements.
Table 1:
(a) Actual positions (b) Measurements (c) Target tracks in terms of
measurement indices
 Time
Time |
n = 1 |
n = 2 |
n = 3 |
 Actual Positions
Actual Positions |
|
|
|
 |
(0,0) |
(1,1.1) |
(2,0) |
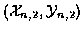 |
(0,2) |
(1,0.9) |
(2,2) |
 Time
Time |
n = 1 |
n = 2 |
n = 3 |
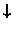 Measurements
Measurements |
|
|
|
| 1 |
(zn,1,1, zn,1,2) |
(0,0) |
(1.9,1.8) |
(0.2,1.6) |
| 2 |
(zn,2,1, zn,2,2) |
(0.4,0.2) |
(1,0.9) |
(2,0) |
| 3 |
(zn,3,1, zn,3,2) |
(0,2) |
(1,1.1) |
(2,2) |
|
Figure 3:
Trellis diagram
 |
Figure 3 shows the trellis structure for this problem. The states at each time instant, representing combinations of the
measurement indices (1,2,3) taken two at a time, are denoted by the pairs
(1,2), (1,3), and (2,3). The best path(s) to any state must also identify
which one of the K! permutations of the measurement indices is being used.
This is facilitated in the trellis structure by having two labels, each of
which is a different permutation of the combination that the state
represents. The states are initialized with 0 path metric at n = 1,
therefore only one permutation is shown. For each state at n = 2 and
n = 3, we keep the best 2 paths to that state. These paths are marked with
dotted-arrows. The numbers at the end of the structure are the path metrics
of the best 2 paths to that state.
We can now pick the overall best two paths, backtrack through the trellis, and easily identify the sets of target tracks that these state transitions correspond to. Table 1(c) lists these tracks in terms of the measurement indices.
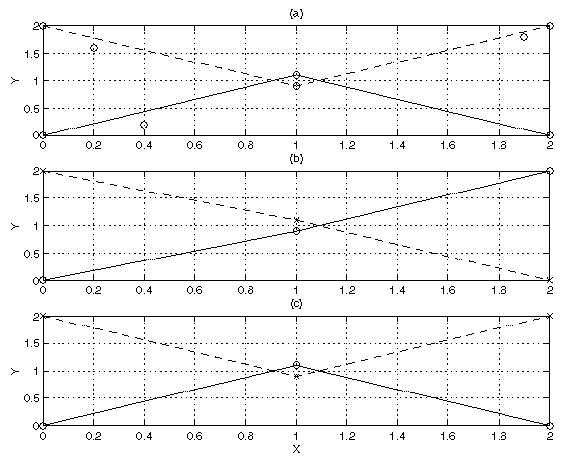
Figure 4(a) shows the measurements (actual positions and clutter).
Figure 4(b) shows the tracks corresponding to the best path. Notice that at n = 2, there is a switch - the lower and upper
estimated tracks follow the upper and lower true tracks, respectively.
Figure 4(c) shows the tracks corresponding to the second best path.
This path has a slightly higher cost, but resembles the true tracks.
Figure 4:
(a) True tracks and clutter Measurements (b) Best two tracks, cost=40 (c) 2nd best two tracks, cost=41
 |
4. An Illustrative Numerical Example
Two parabolic target tracks, consisting of
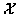 and
and 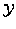 position and velocity values, were generated.
At each of the 21
time instants, two additional random clutter (false alarm) measurements were
generated and random Gaussian noise (variance = 0.01) was added to the target
tracks.
Figure 1 shows the
position and velocity values, were generated.
At each of the 21
time instants, two additional random clutter (false alarm) measurements were
generated and random Gaussian noise (variance = 0.01) was added to the target
tracks.
Figure 1 shows the 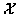 and
and 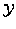 position values for the true
tracks and noisy measurements used as input to the algorithm.
Velocity values are not shown and, for both
tracks,
position values for the true
tracks and noisy measurements used as input to the algorithm.
Velocity values are not shown and, for both
tracks, 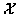 increases with time. Parameter values used
were K=2 and L=16.
increases with time. Parameter values used
were K=2 and L=16.
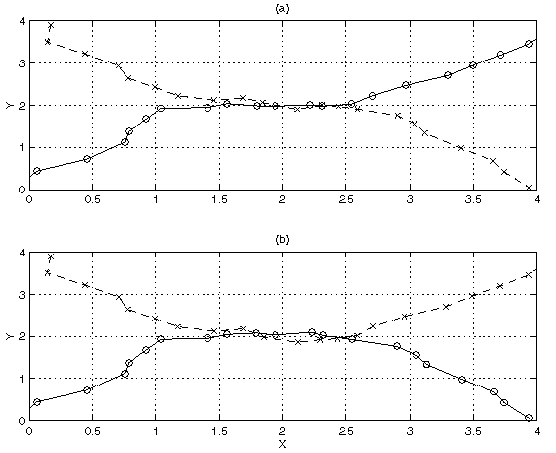
Figure 5(a) shows the best paths.
Note that one path starts out following the
lower parabolic target then switches to the upper target near the
middle of the plot where the target measurements intersect.
The total cost of these best paths is 38.5.
Figure 5(b) shows 7th best paths, which have a cost of 39.3 - just slightly higher than the cost of the best two paths - and correctly follow both the upper and lower parabolic paths.
The 2nd through 6th best paths are not shown, since they
are very similar to the best path and differ only in a few
points.
Our algorithm is able to automatically
determine sets of paths with similar costs and dissimilar trajectories
by examining the norms of path differences. The differences
from the best paths for the 2nd though 16th best paths
shows a large jump at index 7 indicating that the 7th best paths
significantly differ from the best paths in their trajectory.
The cost values for paths 2 through 16 range from 38.7 to 40.3,
all just slightly higher than the best paths.
This example demonstrates the usefulness of examining more than just the
best set of paths. Sets of paths with similar but slightly higher costs,
and dissimilar trajectories, may be passed on to other sensor locations or
a data fusion center which could use combined multisensor data to choose
the overall most likely set of paths.
Figure 5:
(a) Best two tracks, cost=38.5 (b) 7th best two tracks, cost=39.3
 |
5. Conclusions
A novel approach to multitarget tracking, using a trellis structure to find a list of L best sets of K target tracks has been presented. The algorithm described is computationally efficient, and flexibility of the trellis structure facilitates handling track initiation, multiple tracks, false alarms, missed detections and a variety of cost functions. The example presented in Section 4 demonstrates it's usefulness and efficacy in one such model of the problem.



Next: Bibliography
Rick Perry
1998-10-31
![]() candidate tracks.
Let
candidate tracks.
Let
![]() represent these, i.e.
represent these, i.e.
![]() where jm (l) indicates the measurement taken from
time m for track l, and
where jm (l) indicates the measurement taken from
time m for track l, and
![]() is the jm (l)measurement vector at time m. So the candidate track l at time n is
characterized by
is the jm (l)measurement vector at time m. So the candidate track l at time n is
characterized by
![]()
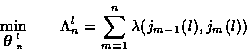
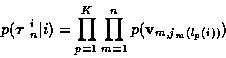
![]() ,
is the solution to the problem:
,
is the solution to the problem:

![]() paths into stage n-1 must be extended to the
paths into stage n-1 must be extended to the
![]() paths into stage n, even though the costs of
some of these paths will indicate that the corresponding K-track sets are
highly unlikely. Alternatively, we propose to keep, at each stage in the
trellis, a ``list'' of only the best (lowest cost) L paths to each state,
where L is selected to assure that no feasible paths are pruned
3.
paths into stage n, even though the costs of
some of these paths will indicate that the corresponding K-track sets are
highly unlikely. Alternatively, we propose to keep, at each stage in the
trellis, a ``list'' of only the best (lowest cost) L paths to each state,
where L is selected to assure that no feasible paths are pruned
3.
