


Next: Time-Independent Gaussian channel
Up: Time-Recursive Maximum Likelihood Based Channels
Previous: Introduction
System model
In the discrete-time FIR model of a time-varying noisy communications channel
with inter-symbol interference, for the received data sequence up to time n,
the complex received data rk at time k is given by
 |
(1) |
where
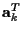 is a complex row vector containing transmitted data
{
is a complex row vector containing transmitted data
{
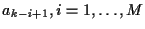 }, M is the FIR channel length,
}, M is the FIR channel length, 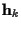 is a complex column vector containing the channel impulse response
coefficients at time k, and nk is the white Gaussian complex noise at
time k with variance
is a complex column vector containing the channel impulse response
coefficients at time k, and nk is the white Gaussian complex noise at
time k with variance 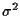 .
Let
.
Let
![${\bf H} = [{\bf h}_1, \ldots , {\bf h}_n]$](img6.gif) represent the matrix
of channel coefficient vectors over time arranged by columns, and
let
represent the matrix
of channel coefficient vectors over time arranged by columns, and
let
![${\bf A} = [{\bf a}_1, \ldots , {\bf a}_n]^T$](img7.gif) represent the
matrix of transmitted data arranged by rows.
Also let
represent the
matrix of transmitted data arranged by rows.
Also let
![${\bf r} = [ r_1 , \ldots , r_n ]^T$](img8.gif) represent the column vector
of received data, and
represent the column vector
of received data, and
![${\bf n} = [ n_1 , \ldots , n_n ]^T$](img9.gif) represent
the column vector of noise over time.
With this notation, the probability density function of the received
data, given
represent
the column vector of noise over time.
With this notation, the probability density function of the received
data, given  and
and 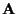 ,
is
,
is
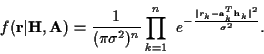 |
(2) |
To minimize BER, we must find
 to maximize
to maximize
 (i.e. the MAP estimator).
This is equivalent to maximizing
(i.e. the MAP estimator).
This is equivalent to maximizing
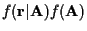 .
If
.
If
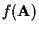 is unknown or assumed to be uniform, then the ML estimator
which maximizes the likelihood function
is unknown or assumed to be uniform, then the ML estimator
which maximizes the likelihood function
 can be used
instead. Referring to (2), if the channel is known, the
Viterbi algorithm can be used directly to estimate the data sequence.
can be used
instead. Referring to (2), if the channel is known, the
Viterbi algorithm can be used directly to estimate the data sequence.
If the channel is unknown,
the dependence of
 on the random channel coefficients is
on the random channel coefficients is
![\begin{displaymath}f({\bf r}\vert{\bf A}) =
E[f({\bf r}\vert{\bf H},{\bf A})] =
...
...} f({\bf r}\vert{\bf H},{\bf A})
f({\bf H }) d{\bf H } \; \; .
\end{displaymath}](img17.gif) |
(3) |
Evaluating this multidimensional integral and then maximizing the result
with respect to 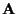 seems to be an intractable problem in general. However, if the statistics
of the channel coefficients can be assumed, it is shown below that in some cases this problem is solvable
and that the Viterbi algorithm or GVA can be applied directly to obtain the optimum or suboptimum results. In the following two sections, we will show how the problem is solved over time-independent Gaussian channels and Gauss-Markov channels.
seems to be an intractable problem in general. However, if the statistics
of the channel coefficients can be assumed, it is shown below that in some cases this problem is solvable
and that the Viterbi algorithm or GVA can be applied directly to obtain the optimum or suboptimum results. In the following two sections, we will show how the problem is solved over time-independent Gaussian channels and Gauss-Markov channels.



Next: Time-Independent Gaussian channel
Up: Time-Recursive Maximum Likelihood Based Channels
Previous: Introduction
Rick Perry
2000-10-29
![]() to maximize
to maximize
![]() (i.e. the MAP estimator).
This is equivalent to maximizing
(i.e. the MAP estimator).
This is equivalent to maximizing
![]() .
If
.
If
![]() is unknown or assumed to be uniform, then the ML estimator
which maximizes the likelihood function
is unknown or assumed to be uniform, then the ML estimator
which maximizes the likelihood function
![]() can be used
instead. Referring to (2), if the channel is known, the
Viterbi algorithm can be used directly to estimate the data sequence.
can be used
instead. Referring to (2), if the channel is known, the
Viterbi algorithm can be used directly to estimate the data sequence.
![]() on the random channel coefficients is
on the random channel coefficients is