


Next: Gauss-Markov channel
Up: Time-Recursive Maximum Likelihood Based Channels
Previous: System model
Time-Independent Gaussian channel
For channel coefficients independent over time,
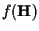 can be expressed
as
can be expressed
as
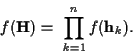 |
(4) |
If
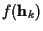 is Gaussian with mean
is Gaussian with mean 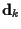 and covariance
and covariance
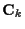 ,
then
,
then
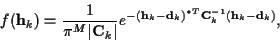 |
(5) |
where * denotes conjugate, M is the FIR channel length and we assume that 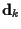 and
and 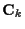 are known.
Substituting (2) and (4) into (3), taking the negative
natural logarithm of the integration result and ignoring the terms that are irrelevant to the minimization, we
obtain:
are known.
Substituting (2) and (4) into (3), taking the negative
natural logarithm of the integration result and ignoring the terms that are irrelevant to the minimization, we
obtain:
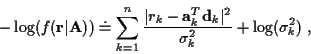 |
(6) |
where
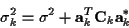 |
(7) |
(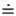 denotes equivalent for optimization purposes).
denotes equivalent for optimization purposes).
The time-recursive form for (6) can be expressed as
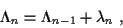 |
(8) |
where
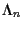 is the cumulative cost up to time n. From (6),
is the cumulative cost up to time n. From (6),
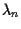 is the incremental cost from time n-1 to n:
is the incremental cost from time n-1 to n:
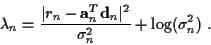 |
(9) |
Since the incremental cost only depends on the state transition at time n,
the Viterbi algorithm can be used directly to minimize (8). Therefore,
(8) represents a computationally efficient, time-recursive, exact MAP (optimum) algorithm.



Next: Gauss-Markov channel
Up: Time-Recursive Maximum Likelihood Based Channels
Previous: System model
Rick Perry
2000-10-29
![]() can be expressed
as
can be expressed
as