Time-Independent Gaussian channel

To illustrate the effectiveness of the computationally efficient, time-recursive algorithm described above for the time-independent, Gaussian model, 10,000 trials were performed for each of several values of SNR from 5 to 17 dB. For each trial, random BPSK transmitted symbol values were generated using a uniform distribution, so the symbol values -1 and 1 were equally likely. A channel FIR length of M=3 was used. The channel coefficients were generated as independent (over time) Gaussian random variables, with mean ${\bf d}_k$ changing linearly from 1 to 2 over the block of time. The following constant channel coefficient covariance

$${\bf C} = v \; \left[ \begin{array}{rrr} 1 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \end{array} \right]$$ (22)

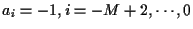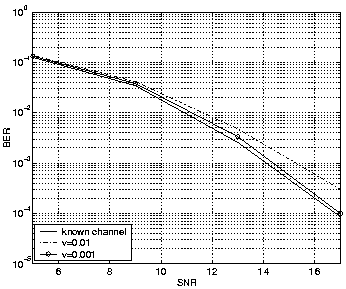
was used, and the initial channel symbols were fixed as $a_{i} = -1, i=-M+2,\cdots,0$. Figure 1 shows the BER vs. SNR for several values of the channel coefficient variance parameter v. When v is smaller, the algorithm performs better, approaching closely the performance of the known channel MLSE.

  

Figure 1: BER vs. SNR for time-varying independent Gaussian channel