


Next: EM for Non-Time-Varying Channels
Up: Sequence Estimation over Linearly-Constrained
Previous: Communication System Model
EM and ML Sequence Estimation
To minimize BER, we must find  to maximize
to maximize
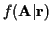 .
Using Bayes rule:
.
Using Bayes rule:
 |
(9) |
where
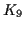 is a constant which takes into account the effect
of
is a constant which takes into account the effect
of
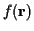 for normalizing the distribution.1
MAP estimators minimize BER by maximizing
for normalizing the distribution.1
MAP estimators minimize BER by maximizing
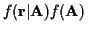 .
If
.
If
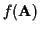 is unknown or assumed to be uniform, then the ML estimator
which maximizes the likelihood function
is unknown or assumed to be uniform, then the ML estimator
which maximizes the likelihood function
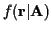 can be used
instead. All of the EM algorithms derived in the subsequent sections produce
iterative solutions to the ML problem of maximizing
can be used
instead. All of the EM algorithms derived in the subsequent sections produce
iterative solutions to the ML problem of maximizing
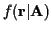 .
But if
.
But if
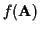 is known and not uniform,
then this could be incorporated into
the following EM algorithms as an additive term in the cost function,
thus producing a MAP estimator.
The dependence of
is known and not uniform,
then this could be incorporated into
the following EM algorithms as an additive term in the cost function,
thus producing a MAP estimator.
The dependence of
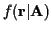 on the underlying random channel
coefficients is:
on the underlying random channel
coefficients is:
![\begin{displaymath}f({\bf r}\vert{\bf A}) =
E[f({\bf r}\vert{\bf P},{\bf A})] =
...
...\bf P}} f({\bf r}\vert{\bf P},{\bf A})
f({\bf P }) d{\bf P } ,
\end{displaymath}](img41.gif) |
(10) |
where
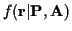 is given by (6)
for time-varying channels. Evaluating this multidimensional integral and
then maximizing the result with respect to
is given by (6)
for time-varying channels. Evaluating this multidimensional integral and
then maximizing the result with respect to  seems to be an
intractable problem in general. Yet this is exactly the problem which EM
algorithms can solve iteratively.
The only apparent case where direct evaluation and maximization of
seems to be an
intractable problem in general. Yet this is exactly the problem which EM
algorithms can solve iteratively.
The only apparent case where direct evaluation and maximization of
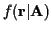 from (10) seems tractable is if
from (10) seems tractable is if 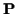 is
non-time-varying and deterministic. Then
is
non-time-varying and deterministic. Then
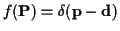 ,
where
,
where 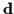 is an unknown
constant,
is an unknown
constant,
 from (3), and (10) reduces to (8)
with
from (3), and (10) reduces to (8)
with
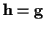 ,
where
,
where 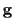 is the deterministic but unknown
value of
is the deterministic but unknown
value of 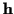 ,
as discussed further in Section 4. This
provides a theoretical basis for the joint
,
as discussed further in Section 4. This
provides a theoretical basis for the joint
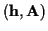 estimation
algorithms such as [1,12,2,4]. However for arbitrary
estimation
algorithms such as [1,12,2,4]. However for arbitrary
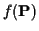 we must work with (10) directly, or
use an EM algorithm, in order to produce optimal estimates of
we must work with (10) directly, or
use an EM algorithm, in order to produce optimal estimates of  .
.
To maximize (10) using EM, define the auxiliary function
[5]:
where we desire the ML estimate of  ,
and
,
and 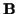 represents the
current estimate of
represents the
current estimate of  .
In the terminology of EM,
.
In the terminology of EM, 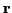 is the
observed data,
is the
observed data, 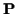 is the hidden data, and
is the hidden data, and
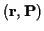 is the
complete data.
is the
complete data.
The general EM algorithm for this problem is:
- 1.
- Initialize
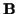 to an estimate of
to an estimate of  .
.
- 2.
- E-step (Expectation): construct

- 3.
- M-step (Maximization): find
 to maximize
to maximize

- 4.
- Set
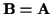 and repeat steps 2 and 3 until converged.
and repeat steps 2 and 3 until converged.
In general, to construct
 ,
start with
,
start with
 :
:
 |
(12) |
We can drop the
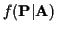 term from this since
term from this since 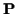 and
and
 are independent so
are independent so
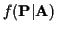 is not a function of
is not a function of
 and will not affect the maximization in the M-step.
and will not affect the maximization in the M-step.
 from (11) may then be written as:
from (11) may then be written as:
To evaluate
 ,
we need
,
we need
 ,
which
can be written in terms of the apriori underlying channel coefficient density
function
,
which
can be written in terms of the apriori underlying channel coefficient density
function
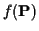 as:
as:
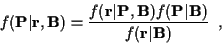 |
(14) |
where the denominator term
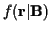 can be treated as a
constant since it simply serves to normalize the distribution, and is not a
function of
can be treated as a
constant since it simply serves to normalize the distribution, and is not a
function of 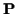 or
or  ,
so will not affect the maximization step.
Also,
,
so will not affect the maximization step.
Also,
 since the underlying channel
coefficients and transmitted data are independent.
But note that given
since the underlying channel
coefficients and transmitted data are independent.
But note that given 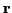 and
and 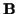 ,
,
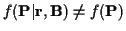 .
Therefore, for
.
Therefore, for
 in (13) we may use:
in (13) we may use:
 |
(15) |
In the specific cases considered subsequently, we will show that the E-step
reduces to computing sufficient statistics of
 ,
which are
the mean and covariance of
,
which are
the mean and covariance of 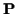 conditioned on
conditioned on 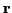 and
and 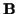 .
This enables the Viterbi algorithm [13] to be used for the M-step.
The Viterbi algorithm is a well-known efficient
method for ML sequence estimation over known channels. It can be used here
in the unknown channel case because of the estimates provided by the E-step.
The E-step and M-step formulas will be derived in detail in subsequent
sections for various specific underlying channel coefficient distributions.
.
This enables the Viterbi algorithm [13] to be used for the M-step.
The Viterbi algorithm is a well-known efficient
method for ML sequence estimation over known channels. It can be used here
in the unknown channel case because of the estimates provided by the E-step.
The E-step and M-step formulas will be derived in detail in subsequent
sections for various specific underlying channel coefficient distributions.



Next: EM for Non-Time-Varying Channels
Up: Sequence Estimation over Linearly-Constrained
Previous: Communication System Model
Rick Perry
2000-03-16