


Next: EM for Time-Varying Channels
Up: Sequence Estimation over Linearly-Constrained
Previous: EM and ML Sequence
EM for Non-Time-Varying Channels
For a non-time-varying channel, using (8) in
(15), (13) becomes:
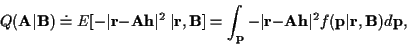 |
(16) |
with
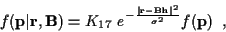 |
(17) |
where
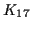 can be determined if needed by setting the
integral of
can be determined if needed by setting the
integral of
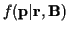 to 1.
To evaluate (16) we only need the mean and covariance of
the channel coefficients
to 1.
To evaluate (16) we only need the mean and covariance of
the channel coefficients 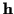 given
given 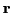 and
and 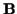 using the distribution of (17).
We will derive these for specific cases of
using the distribution of (17).
We will derive these for specific cases of
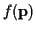 subsequently;
for now, we define them symbolically as
subsequently;
for now, we define them symbolically as 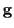 and
and 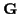 :
:
where 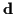 and
and 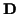 are the mean and covariance of
the underlying channel coefficients
are the mean and covariance of
the underlying channel coefficients 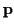 given
given 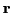 and
and 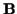 :
:
The noise variance 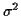 is needed in general to
compute
is needed in general to
compute 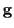 and
and 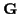 .
If
.
If 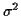 is not known it could be estimated from the variances of the transmitted
and received data.
The norm-squared term in (16), for each candidate
is not known it could be estimated from the variances of the transmitted
and received data.
The norm-squared term in (16), for each candidate 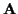 ,
can be represented as a path through a trellis, whose states at a given
time are the states of the of the ISI channel. A path
represents a summation of incremental state transition costs.
The minimum cost path can be determined by the Viterbi algorithm.
Rewriting (16) in terms of the incremental costs:
,
can be represented as a path through a trellis, whose states at a given
time are the states of the of the ISI channel. A path
represents a summation of incremental state transition costs.
The minimum cost path can be determined by the Viterbi algorithm.
Rewriting (16) in terms of the incremental costs:
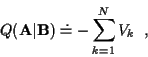 |
(22) |
where Vk is:
![\begin{displaymath}V_k = E[\vert r_k - {\bf a}_k^T {\bf h}\vert^2 \ \vert{\bf r},{\bf B}] \; .
\end{displaymath}](img89.gif) |
(23) |
The expected value is taken over 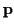 using
(17) for
using
(17) for
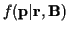 .
Expanding the norm squared, and taking the expected value, yields:
.
Expanding the norm squared, and taking the expected value, yields:
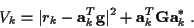 |
(24) |
Equation (24) represents the general form of the Viterbi algorithm
incremental cost function for non-time-varying random ISI channels.
To use (24) in an EM algorithm, 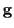 and
and 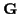 from
(18) and (19) are computed in the M-step; these computations
depend on the specific form of the apriori underlying channel distribution
from
(18) and (19) are computed in the M-step; these computations
depend on the specific form of the apriori underlying channel distribution
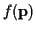 .
The following subsections examine the specific cases of
deterministic, uniform, and Gaussian
.
The following subsections examine the specific cases of
deterministic, uniform, and Gaussian
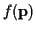 .
.
DETERMINISTIC CHANNEL COEFFICIENTS
The case of deterministic channel coefficients is examined first because
it is the simplest case, and because if there are no constraints it
reduces to previously published algorithms
[1,12,2] which do not use any known apriori statistics
for the channel. Unlike the other cases considered subsequently, for
the deterministic channel we do not know the apriori mean of the
coefficients, and as shown below, the E-step of the EM algorithm
can not use
![$E[{\bf h}\vert{\bf r,B}]$](img91.gif) .
If
.
If 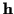 is not random, then let
is not random, then let
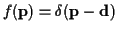 ,
where
,
where 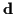 is an unknown constant,
and
is an unknown constant,
and
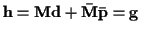 from (3),
where
from (3),
where 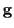 is the deterministic but unknown value of
is the deterministic but unknown value of 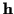 .
In this case,
.
In this case,
![$E[{\bf h}] = {\bf g}$](img94.gif) ,
and using
(17) to estimate
,
and using
(17) to estimate 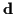 does not
provide anything useful since it reduces to
does not
provide anything useful since it reduces to
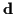 ,
and
,
and 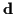 is unknown.
So to estimate
is unknown.
So to estimate 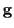 in this case, we must use an ad-hoc method.
Note that given
in this case, we must use an ad-hoc method.
Note that given 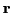 and
and 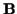 ,
,
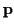 satisfies (7):
satisfies (7):
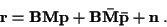 |
(25) |
Taking the expected value of the right-hand-side of (25)
with respect to 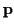 and
and 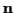 yields:
yields:
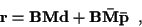 |
(26) |
which can be solved for a linear least-square-error estimate of 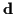 using the pseudo-inverse of
using the pseudo-inverse of 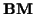 :
:
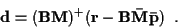 |
(27) |
In this case,
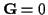 ,
and the Viterbi algorithm incremental cost
function from (24) becomes:
,
and the Viterbi algorithm incremental cost
function from (24) becomes:
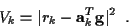 |
(28) |
For the E-step, (27) and (18) are used to estimate 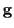 .
For the M-step, the Viterbi algorithm is used with incremental cost function
(28) to estimate
.
For the M-step, the Viterbi algorithm is used with incremental cost function
(28) to estimate 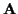 .
For EM initialization, we could select
.
For EM initialization, we could select 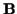 randomly,
or use all 1's, etc. But to reduce the number of iterations required,
and to help the algorithm converge to a proper solution, it is better to
initialize
randomly,
or use all 1's, etc. But to reduce the number of iterations required,
and to help the algorithm converge to a proper solution, it is better to
initialize 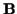 with some reasonable estimate of
with some reasonable estimate of 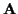 .
This can be
done, for example, by initially using a pure delay channel, i.e. using
.
This can be
done, for example, by initially using a pure delay channel, i.e. using
![${\bf g} = [0 ~ \ldots ~ 0 ~ 1 ~ 0 ~ \ldots ~ 0]^T$](img101.gif) in (28),
then using the Viterbi algorithm to
estimate
in (28),
then using the Viterbi algorithm to
estimate 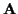 ,
then setting
,
then setting 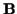 to this estimate of
to this estimate of 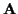 .
Note that if there were no constraints,
or if the constraints were unknown or simply not taken into account,
then
.
Note that if there were no constraints,
or if the constraints were unknown or simply not taken into account,
then
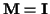 ,
,
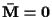 ,
and
,
and
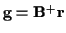 ;
this estimate of
;
this estimate of 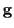 would then be a maximum-likelihood
estimate of
would then be a maximum-likelihood
estimate of 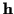 given
given 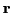 and
and 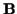 since it maximizes
since it maximizes
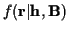 (i.e. minimizes
(i.e. minimizes
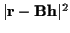 ). The EM algorithm in this case
would be equivalent to previously published algorithms for
optimal joint sequence and channel estimation [1,12,2].
). The EM algorithm in this case
would be equivalent to previously published algorithms for
optimal joint sequence and channel estimation [1,12,2].
UNIFORM UNDERLYING CHANNEL COEFFICIENTS
Using
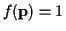 in (17),
in (17),
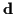 from (27),
and assuming that
from (27),
and assuming that 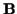 has full rank so that
has full rank so that
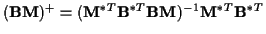 ,
then, dropping constants, we obtain:
,
then, dropping constants, we obtain:
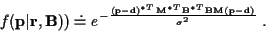 |
(29) |
This shows that, given 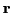 and
and 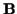 ,
,
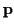 has a joint Gaussian
distribution with mean
has a joint Gaussian
distribution with mean 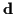 as in (27), and covariance:
as in (27), and covariance:
![\begin{displaymath}{\bf D} =
\left[
\frac { {\bf M}^{*T} {\bf B}^{*T} {\bf B} {\bf M} }
{{\sigma}^2}
\right] ^ {-1} \; \; .
\end{displaymath}](img110.gif) |
(30) |
Therefore, for the case of uniformly distributed underlying channel
coefficients, the EM algorithm is almost the same as for deterministic
channel coefficients, except that the Viterbi algorithm incremental cost
function from (24),
which includes 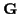 ,
is used instead of (28), and
,
is used instead of (28), and
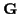 is given by (30) and (19).
For the E-step,
(27) and (30)
are used in (18) and (19)
to estimate
is given by (30) and (19).
For the E-step,
(27) and (30)
are used in (18) and (19)
to estimate
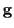 and
and 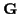 .
For the M-step, the Viterbi algorithm is used with incremental cost function
(24) to estimate
.
For the M-step, the Viterbi algorithm is used with incremental cost function
(24) to estimate 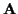 .
.
GAUSSIAN UNDERLYING CHANNEL COEFFICIENTS
Let
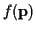 be a joint Gaussian distribution with
mean
be a joint Gaussian distribution with
mean 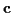 and covariance
and covariance 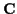 :
:
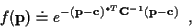 |
(31) |
where 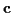 and
and 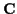 are known. Then (17)
reduces to:
are known. Then (17)
reduces to:
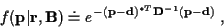 |
(32) |
with:
So in this case, the distribution of 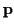 given
given 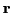 and
and 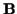 is
also Gaussian. Note that the formulas above for the mean and covariance
of
is
also Gaussian. Note that the formulas above for the mean and covariance
of 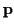 given
given 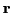 and
and 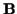 do not use
do not use
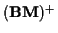 as in the previous
deterministic and uniform cases.
The Gaussian distribution of
as in the previous
deterministic and uniform cases.
The Gaussian distribution of 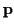 is intermediate between the known
deterministic channel case and uniform unknown
is intermediate between the known
deterministic channel case and uniform unknown 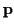 .
In the limit as
.
In the limit as
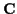 goes to 0,
goes to 0, 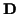 approaches
approaches 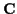 and
and 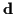 approaches known
approaches known
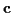 ,
which corresponds to the Gaussian distribution approaching
,
which corresponds to the Gaussian distribution approaching
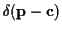 .
This is similar to the deterministic channel
.
This is similar to the deterministic channel
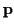 case except that here the mean is known
as opposed to being estimated using (27).
In the limit as
case except that here the mean is known
as opposed to being estimated using (27).
In the limit as 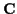 goes to infinity,
goes to infinity, 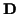 approaches
approaches
![$\left[ \frac {{\bf M}^{*T} {\bf B}^{*T} {\bf B} {\bf M}}{{\sigma}^2}
\right] ^{-1}$](img119.gif) and
and 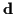 approaches
approaches
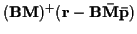 ,
which corresponds to
the Gaussian distribution approaching a uniform distribution.
Also, if N >> L or the noise variance is small,
the term involving
,
which corresponds to
the Gaussian distribution approaching a uniform distribution.
Also, if N >> L or the noise variance is small,
the term involving 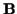 in (33) can dominate the
in (33) can dominate the
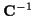 term, and then
term, and then 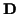 approaches 0,
and
approaches 0,
and 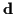 approaches
approaches
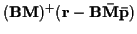 ,
which corresponds to
the Gaussian EM algorithm becoming equivalent to the algorithm
for deterministic channel coefficients.
For the E-step,
(33) and (34)
are used in
(18) and (19)
to estimate
,
which corresponds to
the Gaussian EM algorithm becoming equivalent to the algorithm
for deterministic channel coefficients.
For the E-step,
(33) and (34)
are used in
(18) and (19)
to estimate
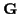 and
and 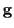 .
For the M-step, the Viterbi algorithm is used with incremental cost function
(24) to estimate
.
For the M-step, the Viterbi algorithm is used with incremental cost function
(24) to estimate 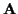 .
.



Next: EM for Time-Varying Channels
Up: Sequence Estimation over Linearly-Constrained
Previous: EM and ML Sequence
Rick Perry
2000-03-16
![]() .
If
.
If ![]() is not random, then let
is not random, then let
![]() ,
where
,
where ![]() is an unknown constant,
and
is an unknown constant,
and
![]() from (3),
where
from (3),
where ![]() is the deterministic but unknown value of
is the deterministic but unknown value of ![]() .
In this case,
.
In this case,
![]() ,
and using
(17) to estimate
,
and using
(17) to estimate ![]() does not
provide anything useful since it reduces to
does not
provide anything useful since it reduces to
![]() ,
and
,
and ![]() is unknown.
So to estimate
is unknown.
So to estimate ![]() in this case, we must use an ad-hoc method.
Note that given
in this case, we must use an ad-hoc method.
Note that given ![]() and
and ![]() ,
,
![]() satisfies (7):
satisfies (7):
![]() in (17),
in (17),
![]() from (27),
and assuming that
from (27),
and assuming that ![]() has full rank so that
has full rank so that
![]() ,
then, dropping constants, we obtain:
,
then, dropping constants, we obtain:
![]() be a joint Gaussian distribution with
mean
be a joint Gaussian distribution with
mean ![]() and covariance
and covariance ![]() :
:
![$\left[ \frac {{\bf M}^{*T} {\bf B}^{*T} {\bf B} {\bf M}}{{\sigma}^2}
\right] ^{-1}$](img119.gif) and
and