


Next: Summary and Conclusions
Up: Sequence Estimation over Linearly-Constrained
Previous: EM for Time-Varying Channels
Simulation Results
For all of the simulations shown here, 20,000 trials were performed for
values of SNR from 0 to 10 in steps of 2, and two iterations of the EM
algorithms were used. For each trial, N = 12 random BPSK transmitted
symbol values were generated using a uniform distribution, so the symbol
values -1 and 1 were equally likely. A channel FIR length of L=4 was used,
the channel was initialized to the known state [-1 -1 -1],
and the true noise variance was used in the algorithms.
The Viterbi algorithm was used to estimate the transmitted symbols and produce
the BER results. For a reference BER, the Viterbi algorithm with known
channel coefficients was used.
The EM algorithms were initialized using the symbol
values as predicted by running the Viterbi algorithm with the true channel
coefficients.
The channel coefficients were constrained to have a double zero at DC
using:
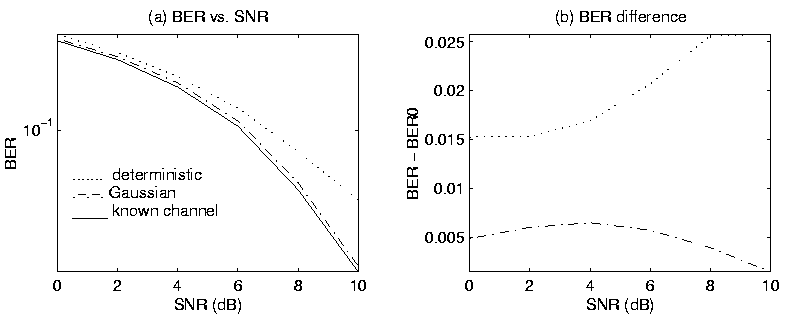
Figure:
1: BER vs. SNR for deterministic and constrained deterministic
EM algorithms using
N = 12, L = 4: (a) absolute BER; (b) BER difference from known channel.
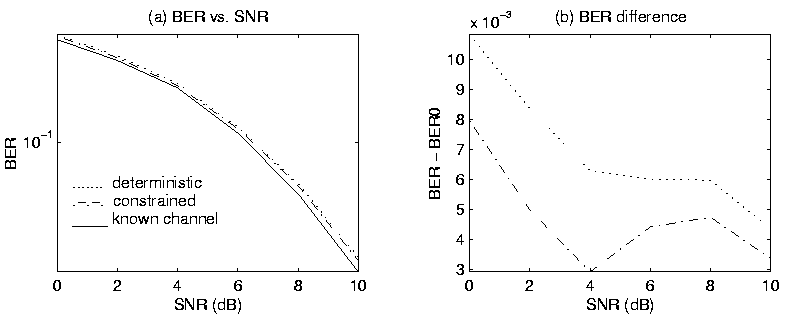 |
For the non-time-varying channel, the first set of
simulation results confirm that the EM algorithm which
incorporates knowledge of the linear constraints
produces lower bit-error-rates in the estimated symbols.
For the simulation results shown in Figure 6,
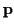 was fixed as [1 1]T.
The ``deterministic'' algorithm performs
optimal joint sequence and channel estimation [1,12,2]
without taking the constraints into account.
was fixed as [1 1]T.
The ``deterministic'' algorithm performs
optimal joint sequence and channel estimation [1,12,2]
without taking the constraints into account.
Figure:
2: BER vs. SNR for deterministic and constrained Gaussian
EM algorithms using
N = 12, L = 4:
(a) absolute BER; (b) BER difference from known channel.
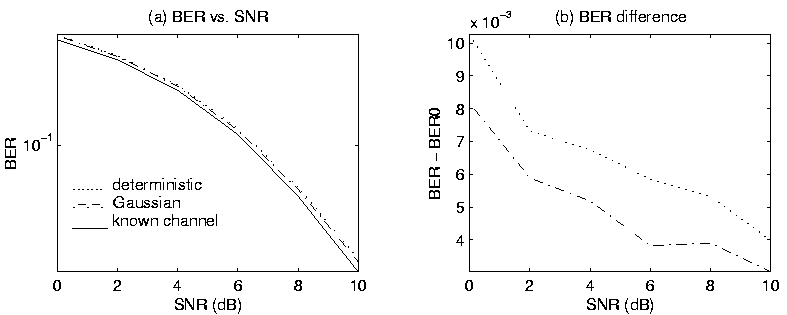 |
In the second set of simulations, the underlying channel coefficients for each trial
were generated as Gaussian random values with mean 1 and covariance
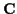 |
= |
![$\displaystyle \left[
\begin{array}{rr}
0.5 & -0.5 \\
-0.5 & 1 \\
\end{array}\right] .$](img184.gif) |
|
The results shown in Figure 2
demonstrate that when the underlying channel coefficients have
a non-time-varying Gaussian distribution,
the Gaussian EM algorithm results in lower BER
as compared with the EM algorithm for unconstrained deterministic channel coefficients.
Figure:
3: BER vs. SNR for deterministic and constrained time-varying
Gaussian EM algorithms using
N = 12, L = 4:
(a) absolute BER; (b) BER difference from known channel.
 |
For time-varying channel coefficients, Figure 3
shows results from a simulation using the Gaussian EM algorithm.
For each trial,
the underlying channel coefficients were generated
as independent (over time) Gaussian random variables,
with mean 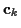 changing linearly from 1 to 2 over the block of time,
and fixed covariance
changing linearly from 1 to 2 over the block of time,
and fixed covariance
 |
= |
![$\displaystyle \left[
\begin{array}{rr}
0.1 & -0.1 \\
-0.1 & 0.2
\end{array}\right] .$](img186.gif) |
|
The Gaussian EM algorithm performs almost as well as the known channel
in this case, and outperforms the deterministic algorithm
dramatically as SNR increases.
Figure:
4: BER vs. SNR for deterministic and constrained Gauss-Markov EM algorithms
using
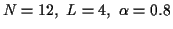 :
(a) absolute BER; (b) BER difference from known channel.
:
(a) absolute BER; (b) BER difference from known channel.
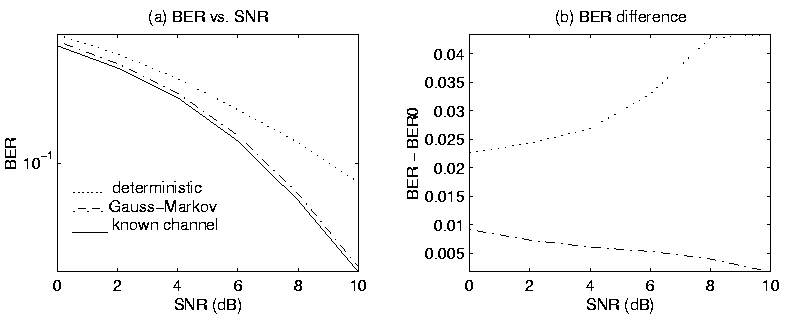 |
For Gauss-Markov channel coefficients, Figure 4
shows results from a typical simulation.
The underlying channel coefficients were generated randomly
using the Gauss-Markov formula (49) with 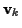 having
mean 0.2 and the same covariance matrix as shown above for the
time-varying Gaussian simulation. The Gauss-Markov EM
algorithm performs almost as well as the known channel case,
and much better than the deterministic algorithm.
having
mean 0.2 and the same covariance matrix as shown above for the
time-varying Gaussian simulation. The Gauss-Markov EM
algorithm performs almost as well as the known channel case,
and much better than the deterministic algorithm.



Next: Summary and Conclusions
Up: Sequence Estimation over Linearly-Constrained
Previous: EM for Time-Varying Channels
Rick Perry
2000-03-16
![$\displaystyle {\bf F} = \left[
\begin{array}{rrrr}
1 & 1 & 1 & 1 \\
0 & 1 & 2 & 3 \\
\end{array}\right] , ~ ~ ~$](img179.gif)
![$\displaystyle {\bf f} = \left[
\begin{array}{r}
0 \\
0 \\
\end{array}\right]
.$](img180.gif)
![$\displaystyle {\bf F} = \left[
\begin{array}{rrrr}
1 & 1 & 1 & 1 \\
0 & 1 & 2 & 3 \\
\end{array}\right] , ~ ~ ~$](img179.gif)
![$\displaystyle {\bf f} = \left[
\begin{array}{r}
0 \\
0 \\
\end{array}\right]
.$](img180.gif)

![]() was fixed as [1 1]T.
The ``deterministic'' algorithm performs
optimal joint sequence and channel estimation [1,12,2]
without taking the constraints into account.
was fixed as [1 1]T.
The ``deterministic'' algorithm performs
optimal joint sequence and channel estimation [1,12,2]
without taking the constraints into account.

![$\displaystyle \left[
\begin{array}{rr}
0.5 & -0.5 \\
-0.5 & 1 \\
\end{array}\right] .$](img184.gif)

![$\displaystyle \left[
\begin{array}{rr}
0.1 & -0.1 \\
-0.1 & 0.2
\end{array}\right] .$](img186.gif)

![]() having
mean 0.2 and the same covariance matrix as shown above for the
time-varying Gaussian simulation. The Gauss-Markov EM
algorithm performs almost as well as the known channel case,
and much better than the deterministic algorithm.
having
mean 0.2 and the same covariance matrix as shown above for the
time-varying Gaussian simulation. The Gauss-Markov EM
algorithm performs almost as well as the known channel case,
and much better than the deterministic algorithm.