


Next: Simulation Results
Up: Sequence Estimation over Linearly-Constrained
Previous: EM for Non-Time-Varying Channels
EM for Time-Varying Channels
For a time-varying channel, using (6) in
(15) and dropping constants, (13) becomes:
with:
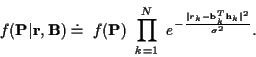 |
(36) |
In this time-varying case, in the E-step of the EM algorithm, time varying
channel impulse response vector conditional means and covariances will be
estimated.
The details of the EM algorithm in this case depend on the form of
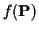 .
The following subsections examine the specific cases of
independent and independent Gaussian underlying channel coefficient
distributions.
.
The following subsections examine the specific cases of
independent and independent Gaussian underlying channel coefficient
distributions.
INDEPENDENT UNDERLYING CHANNEL COEFFICIENTS
If the elements of 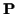 are independent over time, then
are independent over time, then
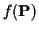 can
be written as:
can
be written as:
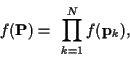 |
(37) |
and
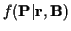 becomes:
becomes:
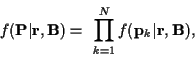 |
(38) |
with:
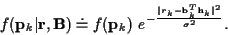 |
(39) |
Using (38) and (39) in
(35) we obtain:
with:
Vk represents the Viterbi algorithm incremental cost function at time k.
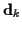 and
and 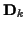 are the mean and covariance of
the underlying channel coefficients
are the mean and covariance of
the underlying channel coefficients 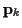 given
given 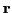 and
and 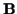 :
:
In the E-step, (41) and (42) will be used to estimate
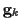 and
and 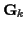 ,
,
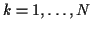 .
In the M-step, the Viterbi algorithm with incremental cost function
(43) will be used to estimate
.
In the M-step, the Viterbi algorithm with incremental cost function
(43) will be used to estimate 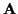 .
To initialize
.
To initialize 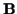 in step 1, we can initialize
in step 1, we can initialize
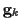 and
and 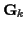 ,
,
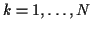 ,
then use the Viterbi algorithm to
estimate
,
then use the Viterbi algorithm to
estimate 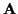 ,
then set
,
then set
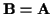 .
To initialize and estimate
.
To initialize and estimate 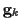 and
and 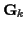 in steps 1 and 2 of the algorithm, we need to know the specific form of
in steps 1 and 2 of the algorithm, we need to know the specific form of
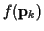 .
The next subsection derives the specific EM algorithm
for Gaussian
.
The next subsection derives the specific EM algorithm
for Gaussian 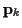 .
.
GAUSSIAN UNDERLYING CHANNEL COEFFICIENTS
If
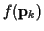 is Gaussian with mean
is Gaussian with mean 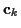 and covariance
and covariance
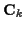 ,
then similar to the derivation of (32)
for the non-time-varying Gaussian case, we obtain:
,
then similar to the derivation of (32)
for the non-time-varying Gaussian case, we obtain:
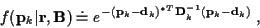 |
(46) |
with:
For the E-step, (47) and (48) are used
in (41) and (42)
to estimate 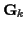 and
and 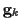 ,
,
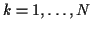 .
For the M-step, the Viterbi algorithm is used with incremental cost function
(43) to estimate
.
For the M-step, the Viterbi algorithm is used with incremental cost function
(43) to estimate 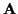 .
.
GAUSS-MARKOV UNDERLYING CHANNEL COEFFICIENTS
For a fast time-varying channel with Gauss-Markov fading parameters,
let 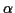 represent a complex first-order Markov factor such that
represent a complex first-order Markov factor such that
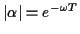 where T is the sampling period and
where T is the sampling period and
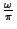 is the Doppler spread [14].
Let the time-varying underlying channel coefficients follow a Gauss-Markov
distribution such that, at time k:
is the Doppler spread [14].
Let the time-varying underlying channel coefficients follow a Gauss-Markov
distribution such that, at time k:
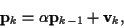 |
(49) |
where 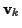 is complex, white, and Gaussian
with mean
is complex, white, and Gaussian
with mean 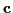 and covariance
and covariance 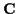 .
In this case,
.
In this case,
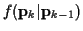 is Gaussian with mean
is Gaussian with mean
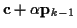 and covariance
and covariance 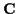 .
.
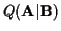 from (35) can be written in terms of
from (35) can be written in terms of
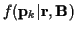 :
:
and the definitions of 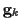 ,
,
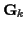 ,
and Vk from
(41-43) still apply.
,
and Vk from
(41-43) still apply.
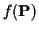 can be written as:
can be written as:
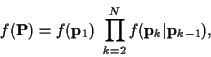 |
(51) |
so
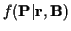 from (36) becomes:
from (36) becomes:
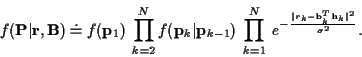 |
(52) |
To determine
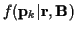 ,
and thereby
,
and thereby 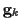 and
and 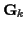 ,
we must integrate
(52) over
,
we must integrate
(52) over
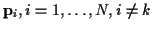 .
Due to space limitations, the derivation of this integration result is not
shown here. A derivation for the same problem, but without the linear
constraints, appears in [15].
The result is that
.
Due to space limitations, the derivation of this integration result is not
shown here. A derivation for the same problem, but without the linear
constraints, appears in [15].
The result is that
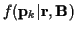 is Gaussian,
with mean
is Gaussian,
with mean 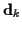 and covariance
and covariance 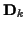 determined by the following
recursive algorithm:
determined by the following
recursive algorithm:
Initialize: for
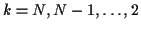
Iterate: for
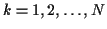
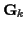 and
and 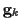 from above
will be used in the Viterbi algorithm incremental cost function for time k.
from above
will be used in the Viterbi algorithm incremental cost function for time k.
- Update for next iteration:
with
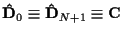 ,
,
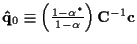 ,
and
,
and
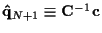 .
It is apparent from the above algorithm that
.
It is apparent from the above algorithm that
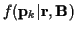 at any time kdepends on all of the received data and estimated symbols from time 1 to N.
For the E-step, the algorithm from (53-55)
is used to estimate
at any time kdepends on all of the received data and estimated symbols from time 1 to N.
For the E-step, the algorithm from (53-55)
is used to estimate 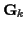 and
and 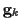 ,
,
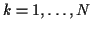 .
For the M-step, the Viterbi algorithm is used with incremental cost function
(43) to estimate
.
For the M-step, the Viterbi algorithm is used with incremental cost function
(43) to estimate 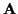 .
.



Next: Simulation Results
Up: Sequence Estimation over Linearly-Constrained
Previous: EM for Non-Time-Varying Channels
Rick Perry
2000-03-16
![$\displaystyle E[\ - \sum_{k=1}^{N} \vert r_k-{\bf a}_k^{T}{\bf h}_k\vert^{2} \
\vert {\bf r},{\bf B}]$](img122.gif)
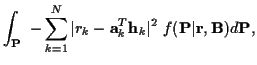
![]() are independent over time, then
are independent over time, then
![]() can
be written as:
can
be written as:
![]() is Gaussian with mean
is Gaussian with mean ![]() and covariance
and covariance
![]() ,
then similar to the derivation of (32)
for the non-time-varying Gaussian case, we obtain:
,
then similar to the derivation of (32)
for the non-time-varying Gaussian case, we obtain:
![]() represent a complex first-order Markov factor such that
represent a complex first-order Markov factor such that
![]() where T is the sampling period and
where T is the sampling period and
![]() is the Doppler spread [14].
Let the time-varying underlying channel coefficients follow a Gauss-Markov
distribution such that, at time k:
is the Doppler spread [14].
Let the time-varying underlying channel coefficients follow a Gauss-Markov
distribution such that, at time k: