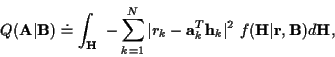 |
(7) |
Using (2) in (6) and dropping constants:
As an intermediate development, first assume that the elements of ![]() are independent over time. Then
are independent over time. Then
![]() can be written as
can be written as
![]() ,
and
,
and
![]() becomes:
becomes:
Now, for a fast time-varying channel with Gauss-Markov fading parameters,
let ![]() represent a complex first-order Markov factor such that
represent a complex first-order Markov factor such that
![]() where T is the sampling period and
where T is the sampling period and
![]() is the Doppler spread [17].
Let the time-varying channel coefficients follow a Gauss-Markov
distribution such that, at time k:
is the Doppler spread [17].
Let the time-varying channel coefficients follow a Gauss-Markov
distribution such that, at time k:
(11) and the definitions from
(12-14) still apply, with:
Initialize: for
![]()
Iterate: for
![]()
It is apparent from the above algorithm that
![]() at any time kdepends on all of the received data and estimated symbols from time 1 to N.
In the EM algorithm E-step, (17-19) are used
to estimate
at any time kdepends on all of the received data and estimated symbols from time 1 to N.
In the EM algorithm E-step, (17-19) are used
to estimate ![]() and
and ![]() ,
,
![]() .
In the M-step, the Viterbi algorithm with incremental cost function
(14) is used to estimate
.
In the M-step, the Viterbi algorithm with incremental cost function
(14) is used to estimate ![]() .
.