


Next: Conclusion
Up: A New Pruning/Merging Algorithm
Previous: Additional Hypothesis Merging and
Letting
Jm = Tmi + Fmi, where
Tmi is the number of measurement vectors at time m used in the Ktrack set
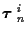 and Fmi is the number of assumed
false alarms, we have that
and Fmi is the number of assumed
false alarms, we have that
 |
(16) |
where
p( Fmi ) is the Poisson distributed probability of Fmifalse alarms. Then, referring to (13), the a priori
incremental cost is
First,
two parabolic target tracks consisting of n=21 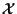 and
and 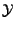 position values were generated. Gaussian
measurement noise with a variance of 0.01 was
added to the target tracks. ``False detect'' events were generated using a
Poisson distribution with a false alarm rate of 2, and the false detections
themselves were generated using a uniform distribution over the range
[0,4]. Probability of detection was assumed to be 0.7, and
for the purpose of illustrating that our algorithm can ``regain'' a target
even after a series of missed detections, the lower track was forced to
have missed detections from
position values were generated. Gaussian
measurement noise with a variance of 0.01 was
added to the target tracks. ``False detect'' events were generated using a
Poisson distribution with a false alarm rate of 2, and the false detections
themselves were generated using a uniform distribution over the range
[0,4]. Probability of detection was assumed to be 0.7, and
for the purpose of illustrating that our algorithm can ``regain'' a target
even after a series of missed detections, the lower track was forced to
have missed detections from
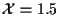 to 2.5. Other simulation
parameters were K=2 and L=16.
Figure 2 shows the
to 2.5. Other simulation
parameters were K=2 and L=16.
Figure 2 shows the 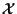 and
and 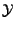 position
values for the true tracks, and the noisy measurements used as input to the
algorithm.
position
values for the true tracks, and the noisy measurements used as input to the
algorithm.
Figure 2:
True Tracks and Measurements
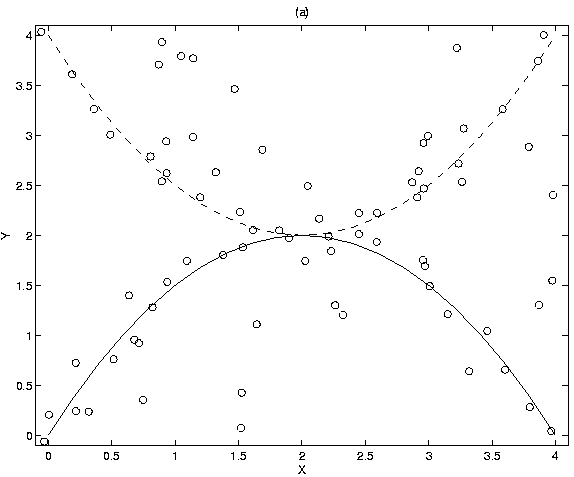 |
Figure 3 shows the best paths, the total cost of which is
117.35. Notice that the one track starts out following the lower
target, but switches to the upper target around the region where the true
tracks intersect. Figure 4 shows the fourth best paths,
which have a total cost of 118.41, just slightly higher than the cost of the
best paths, and which correctly follow both the targets. Notice that during
missed-detect events, the lower track follows a path tangential to the
true track, but ``regains'' the target again when detections are recorded.
Figure 3:
Best set of two tracks, cost=117.35
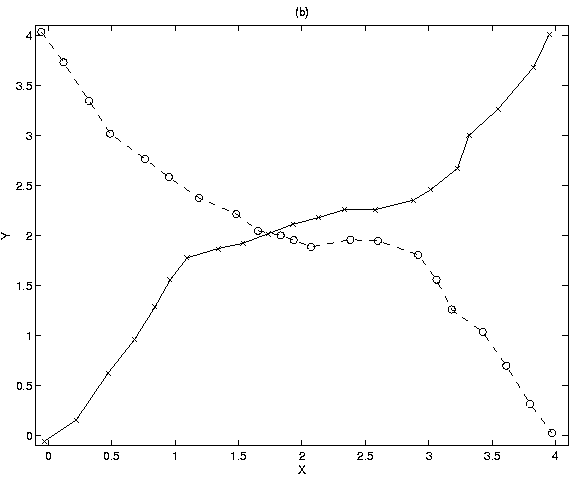 |
Figure 4:
4th best set of two tracks, cost=118.41.
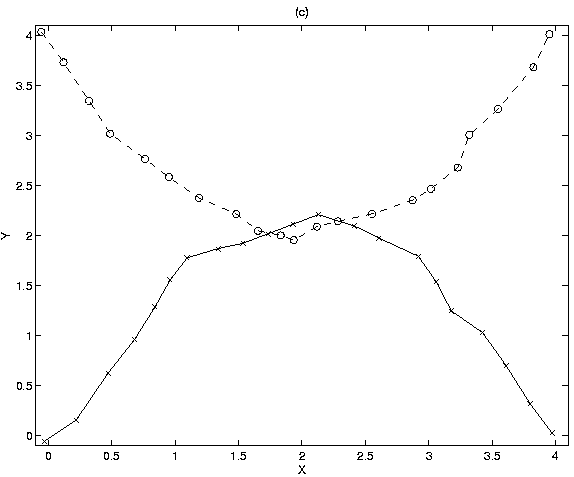 |
Figure 5:
Single Track with Missed Target Events:
(a) true track and measurements with false detections;
(b) estimated track vs. values of L and merging strategy.
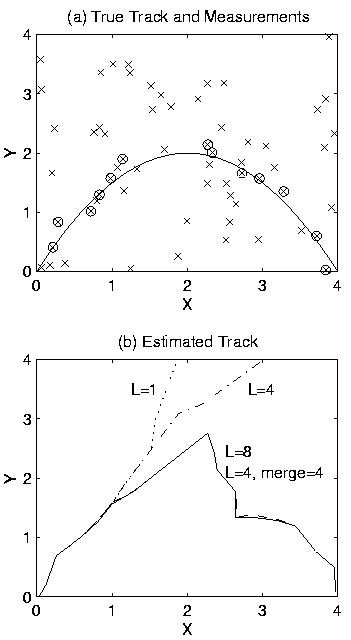 |
For the second simulation,
Figure 5(a) shows an example scenario with a single
target traveling in the positive X direction vs. time. In this figure,
the solid line is the true target track. ``x''
marks the positions of false detections, which were generated randomly
and uniformly over the observation space
with a Poisson distribution average of two false detections per unit time.
The ``x'''s enclosed in circles represent measurements associated with
the target, generated using a noise variance of 0.01. Four sequential
missed target events occur in the range
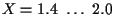 ,
and
three additional missed target events occur in the range
,
and
three additional missed target events occur in the range
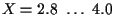 .
The probability of detection is 0.6.
.
The probability of detection is 0.6.
Figure 5(b) shows the tracks produced by running our algorithm
for various values of L and path merging strategy. The track labeled
L=1 is from the standard Viterbi algorithm, and the tracks labeled
L=4 and L=8 are from our List Viterbi algorithm with no path merging.
For L=1 and L=4, the estimated tracks diverge from the true track
as soon as the first missed target events occur; they follow
the linear predictions from the Kalman filter and/or false detections.
For L=8, the estimated track starts to diverge from the true track
for 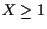 ,
then reacquires the true track for
,
then reacquires the true track for 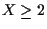 .
.
The track labeled L=4, merge=4, is from our List Viterbi algorithm
using a track merging period of 4. This track is indistinguishable from
the L=8 track, and reacquires the true track with a lower computational
and memory cost.



Next: Conclusion
Up: A New Pruning/Merging Algorithm
Previous: Additional Hypothesis Merging and
Rick Perry
2000-05-06


![]() ,
then reacquires the true track for
,
then reacquires the true track for ![]() .
.