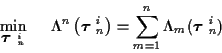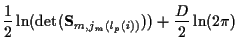Next: The MHT Viterbi Algorithm
Up: A New Pruning/Merging Algorithm
Previous: MAP Based Track Estimation
To derive an equivalent cost from which a time recursive trellis structure
representation can be derived, take the negative natural log of
(6), ignoring
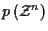 .
For the ith track set, the following equivalent MAP optimization
problem is obtained:
.
For the ith track set, the following equivalent MAP optimization
problem is obtained:
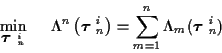 |
(12) |
where the time m incremental cost is
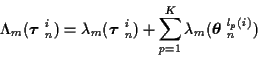 |
(13) |
where
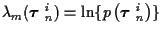 and the pth track incremental cost at time m is
and the pth track incremental cost at time m is
For K track estimation, under the
assumptions that tracks can not share detections,
and that missed detections (as many as K) are possible,
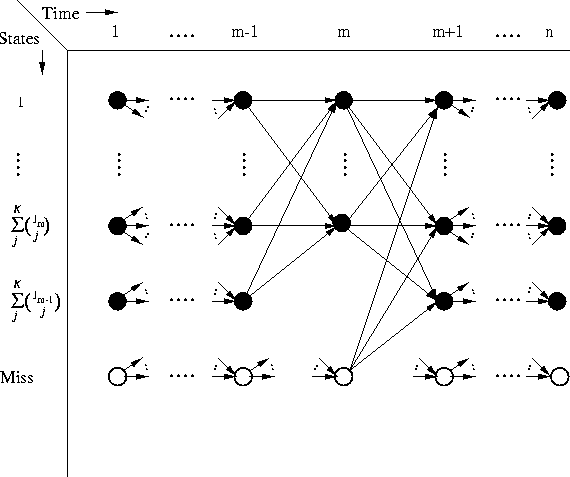
we choose a trellis, depicted in Figure 1,
in which each state represents a set of K measurements and/or
missed measurements. (This is the trellis used in [18].)
For stage m with Jm measurements, there are
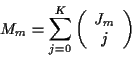 |
(15) |
states. Each branch from stage m-1 to m has a set of
K!/(K-Tmi )!permutations associated with it, specifying the possible orders in which
the K measurements and/or missed measurements represented by the state at
stage m are used5.
Now for each hypothesized K-track set, the incremental cost assigned to a
branch is the sum of the costs of K hypothesized tracks. So, for
hypothesized K-track set
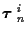 ,
the branch cost from
stage m-1 to m is
,
the branch cost from
stage m-1 to m is
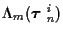 .
The MAP K-track estimation problem is now one
of finding the minimum-cost path through this trellis.
.
The MAP K-track estimation problem is now one
of finding the minimum-cost path through this trellis.
Figure 1:
Trellis Diagram for general K.
 |



Next: The MHT Viterbi Algorithm
Up: A New Pruning/Merging Algorithm
Previous: MAP Based Track Estimation
Rick Perry
2000-05-06