


Next: Trellis Diagram Formulation
Up: A New Pruning/Merging Algorithm
Previous: Hypothesized Track Sets
Using a MAP formulation which incorporates prior track set probabilities, at
time n we have the following optimization problem for determining the
measurement-to-track associations. For
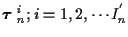
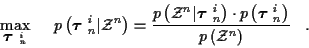 |
(6) |
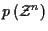 is a normalizing factor which
serves to make the possible values of
is a normalizing factor which
serves to make the possible values of
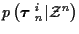 sum to
unity, and can be ignored since it is independent of
sum to
unity, and can be ignored since it is independent of
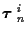 .
.
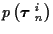 is the a priori probability
of the set of tracks, and is derived from knowledge of the sensors,
targets, noise, clutter, jammers and preprocessors, as manifested for example
as the probability of missed detections and the false alarm rate.
is the a priori probability
of the set of tracks, and is derived from knowledge of the sensors,
targets, noise, clutter, jammers and preprocessors, as manifested for example
as the probability of missed detections and the false alarm rate.
 is the joint probability density function of the measurements
is the joint probability density function of the measurements
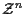 conditioned on the track set
conditioned on the track set
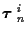 .
For a given
.
For a given
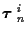 ,
we can
partition
,
we can
partition
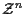 into the data associated with the
tracks,
into the data associated with the
tracks,
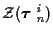 ,
and data associated with
false alarms,
,
and data associated with
false alarms,
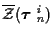 .
We then have
.
We then have
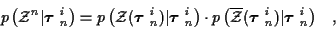 |
(7) |
where, under the assumption that false alarms are uniformly distributed
over the surveillance volume Y,
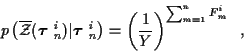 |
(8) |
where Fmi is the number of false alarms at time m given hypothesized
track set
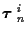 .
In terms of the Kalman filter generated measurement innovations, for the
track measurements,
.
In terms of the Kalman filter generated measurement innovations, for the
track measurements,
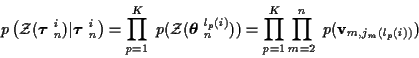 |
(9) |
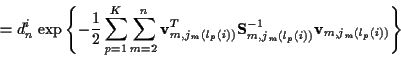 |
(10) |
where for each track p the product (or sum) over m does not include
any missed detections since as noted earlier measurements and innovations
for missed detections do not exist. Keeping this in mind,
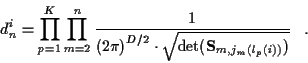 |
(11) |
The MAP cost for estimating the best K tracks is described by
(6), along with
(8), (10), (11) and a
specific form of
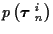 .
.



Next: Trellis Diagram Formulation
Up: A New Pruning/Merging Algorithm
Previous: Hypothesized Track Sets
Rick Perry
2000-05-06