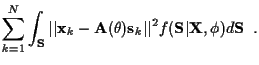Next: Temporally Independent Signal Amplitudes
Up: Maximum Likelihood Source Localization
Previous: EM and ML Source
EM Algorithms for Source Localization
Here we show that the E-step
reduces to computing sufficient statistics of
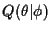 ,
which
are the mean and covariance of
,
which
are the mean and covariance of 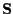 conditioned on
conditioned on 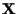 and
and
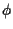 .
This enables the use of an ML-like estimator of
.
This enables the use of an ML-like estimator of 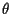 in the
M-step, which employs the sufficient statistics provided in the E-step.
From (8) and (3),
the auxiliary function
in the
M-step, which employs the sufficient statistics provided in the E-step.
From (8) and (3),
the auxiliary function
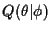 is
is
For each k, the conditional expectation over 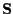 is of the second
order function
is of the second
order function
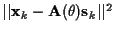 .
It can be shown that this reduces to:
.
It can be shown that this reduces to:
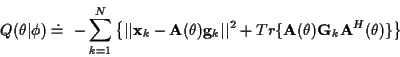 |
(12) |
where
![\begin{displaymath}{\bf g}_k \stackrel{\triangle}{=}
E[{\bf s}_k \vert {\bf X}, \phi ]
\end{displaymath}](img56.gif) |
(13) |
and
![\begin{displaymath}{\bf G}_k \stackrel{\triangle}{=}
E[({\bf s}_k - {\bf g}_k) ({\bf s}_k - {\bf g}_k)^{H}
\vert {\bf X}, \phi ]
\end{displaymath}](img57.gif) |
(14) |
are, respectively, the mean and covariance of the  conditioned on
conditioned on
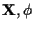 .
A key point is that,
to evaluate (12), we need only the means and covariances of
the
.
A key point is that,
to evaluate (12), we need only the means and covariances of
the  given
given 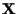 and
and 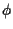 using the distribution of
(9).
We will derive these for specific cases of
using the distribution of
(9).
We will derive these for specific cases of
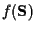 subsequently.
The noise variance
subsequently.
The noise variance 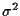 is needed in general to
compute the
is needed in general to
compute the  and
and  .
The EM algorithm is as described generally in Section 3 above, where the
E-step reduces simply to the computation of the
.
The EM algorithm is as described generally in Section 3 above, where the
E-step reduces simply to the computation of the  and the
and the
 .
To initialize
.
To initialize 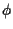 in step 1, we can initialize
in step 1, we can initialize
 and
and  ,
,
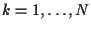 ,
maximize (12) to estimate
,
maximize (12) to estimate 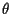 ,
then
set
,
then
set
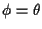 .
To initialize and estimate
.
To initialize and estimate  and
and  in steps 1 and 2 of the algorithm, we need to know the specific form of
in steps 1 and 2 of the algorithm, we need to know the specific form of
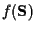 .
.



Next: Temporally Independent Signal Amplitudes
Up: Maximum Likelihood Source Localization
Previous: EM and ML Source
Rick Perry
2000-03-16
![$\displaystyle E[~ - \sum_{k=1}^{N} \vert\vert{\bf x}_k - {\bf A} ( \theta ) {\bf s}_k \vert\vert^{2} ~ \vert
{\bf X}, \phi ]$](img51.gif)
![$\displaystyle \sum_{k=1}^{N}
E[ \vert\vert{\bf x}_k - {\bf A} ( \theta ) {\bf s}_k\vert\vert^{2} ~ \vert {\bf X}, \phi ]$](img52.gif)