Simulation Results

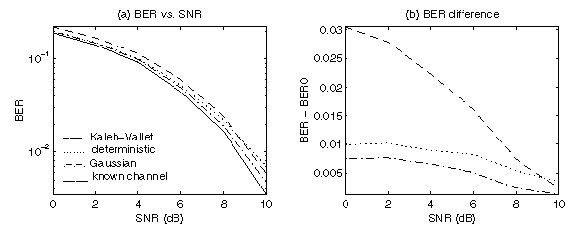
For the simulations shown here, 20,000 trials were performed for values of SNR from 0 to 10 in steps of 2, and 4 iterations of the EM algorithms were used. For each trial, random BPSK transmitted symbol values were generated using a uniform distribution, so the symbol values -1 and 1 were equally likely. A channel FIR length of L=3 was used, the channel coefficients were generated randomly for each trial, and the channel was initialized to the known state [-1 -1]. The true noise variance was used for all algorithms.

The Viterbi algorithm, with truncation of the Viterbi trellis at N - L, was used to estimate the transmitted symbols and produce the BER results. This means that for N=10 and L=3, only errors in the first 7 symbols were used in computing BER. For a reference BER, the Viterbi algorithm with known channel coefficients was used.

For comparison purposes, the EM algorithm from [5] was used, and is referred to as ``Kaleh-Vallet'' in the simulation results. The Kaleh-Vallet algorithm produces optimal estimates of the channel coefficients for data blocks which are short enough such that the channel coefficients are non-time-varying over the block. Also for comparison, the algorithm referred to as ``deterministic'' is that from Section 4.1, and is equivalent to optimal joint sequence and channel estimation [3]. Our EM algorithm for Gaussian channel coefficient distributions (from Section 4.3 is referred to as ``Gaussian'', and produces optimal estimates of the symbols by marginalizing over the channel coefficient distribution.

The deterministic and Gaussian EM algorithms require an initial estimate of the transmitted symbols. For the simulations shown here, these EM algorithms were initialized using the symbol values as predicted by running the Viterbi algorithm with the true channel coefficients. The Kaleh-Vallet EM algorithm requires an initial estimate of the channel coefficients, and was initialized using the true channel coefficients. In the simulations presented here, the EM algorithms converged sufficiently within just about two or three iterations, so four iterations were used for all of the Monte-Carlo simulation runs.

  

Figure 1: BER vs. SNR for deterministic, Gaussian, and Kaleh-Vallet EM algorithms using N = 10,   L = 3: (a) absolute BER; (b) BER difference from known channel.

The simulation results in Figure 1 confirm that knowledge of $f({\bf h})$ as used in the EM algorithm for Gaussian ${\bf h}$ can produce lower bit-error-rates in the estimated symbols. When ${\bf h}$ has a Gaussian distribution, the EM algorithm for Gaussian ${\bf h}$ from Section 4.3 results in lower BER as compared with the EM algorithm for deterministic ${\bf h}$ from Section 4.1, and also performs better than the Kaleh-Vallet algorithm. For this simulation, the channel coefficients were generated as Gaussian random values with mean 1 and covariance:

$${\bf C} \left[ \begin{array}{rrr} 0.5 & -0.5 & 0 \\ -0.5 & 1 & -0.5 \\ 0 & -0.5 & 1 \end{array}\right] .$$ =